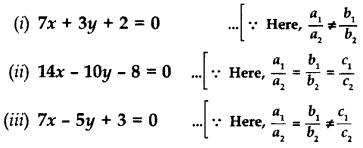Bihar Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Subjective Questions

 

दो चर वाले रैखिक समीकरणों की जोड़ी कक्षा 10 महत्वपूर्ण प्रश्न बहुत ही संक्षिप्त उत्तर (1 अंक)

प्रश्न 1.
समीकरण y = 0 और y = -5 के युग्म के कितने हल हैं? (2013)
हल:
y = 0 और y = -5 समानांतर रेखाएँ हैं, इसलिए कोई हल नहीं है।

प्रश्न 2.
यदि ax + by = a 2 – b 2 और bx + ay = 0, तो (x + y) का मान ज्ञात कीजिए। (2013)
समाधान: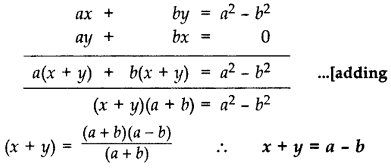

प्रश्न 3.
k के किस मान के लिए, समीकरण युग्म 4x - 3y = 9, 2x + ky = 11 का कोई हल नहीं है? (2017D)
हल:
हमारे पास 4x - 3y = 9 और 2x + ky = 11 . है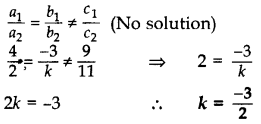

प्रश्न 4.
रेखा x + y = 10 और दोनों निर्देशांक अक्षों से घिरे क्षेत्रफल की गणना कीजिए। (2012)
हल: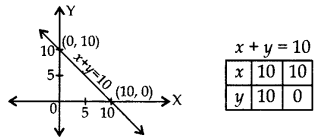

त्रिभुज का क्षेत्रफल
=12× आधार × संगत ऊँचाई
=12× 10 × 10 = 50 सेमी 2

दो चर वाले रैखिक समीकरणों का युग्म कक्षा 10 महत्वपूर्ण प्रश्न संक्षिप्त उत्तर -1 (2 अंक)

प्रश्न 5.
ज्ञात कीजिए कि रैखिक समीकरणों का निम्नलिखित युग्म संगत है या असंगत: (2015)
3x + 2y = 8 6x - 4y = 9
हल: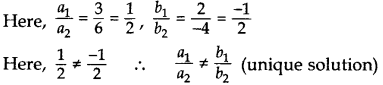

इसलिए दिया गया रैखिक समीकरण युग्म संगत है।

प्रश्न 6.
आलेखीय रूप से जाँच कीजिए कि क्या समीकरणों का युग्म 3x - 2y + 2 = 0 और . है32x - y + 3 = 0, संगत है। उन बिंदुओं के निर्देशांक भी ज्ञात कीजिए जहाँ समीकरणों के ग्राफ़ Y-अक्ष से मिलते हैं।
हल: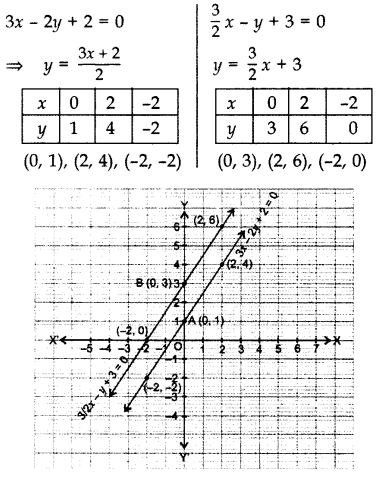

बिन्दुओं को आलेखित करके और उन्हें मिलाने से रेखाएँ कहीं भी प्रतिच्छेद नहीं करती हैं, अर्थात वे समानांतर होती हैं।
इसलिए दिया गया समीकरण युग्म संगत नहीं है, अर्थात असंगत है।
समीकरण 3x - 2y + 2 = 0, Y-अक्ष को A(0,1) पर मिलता है।
समीकरण32x - y + 3 = 0, Y-अक्ष को B(0, 3) पर मिलता है।

प्रश्न 7. 2y = 4x - 6
का आलेख खींचिए;
2x = y + 3 और निर्धारित करें कि रैखिक समीकरणों की इस प्रणाली का एक अद्वितीय समाधान है या नहीं।
हल: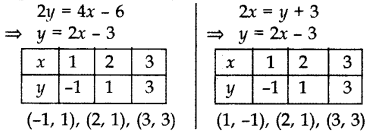


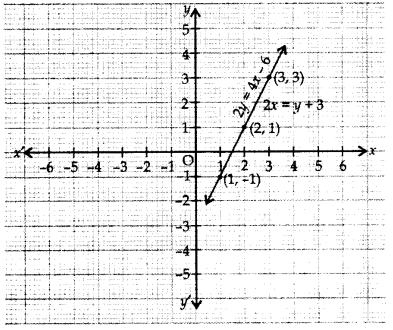
चूँकि दोनों रेखाएँ संपाती होती हैं।
इसलिए असीम रूप से कई समाधान।

प्रश्न 8.
निम्नलिखित समीकरण युग्म को आलेखीय रूप से निरूपित कीजिए और उन बिंदुओं के निर्देशांक लिखिए जहाँ रेखाएँ y-अक्ष को प्रतिच्छेद करती हैं।
हल: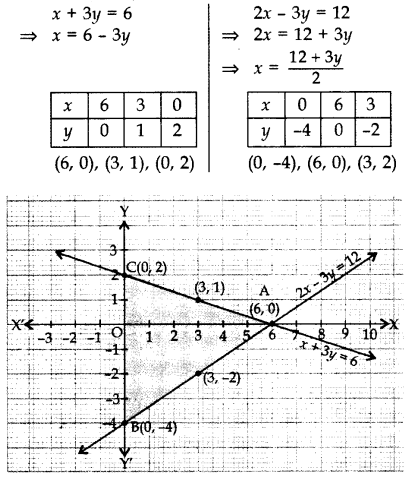

बिन्दुओं को आलेखित करके और उन्हें मिलाने पर रेखाएँ A (6, 0) पर प्रतिच्छेद करती हैं।
रेखा x + 3y = 6 y-अक्ष को B(0, 2) पर और रेखा 2x - 3y = 12 को y-अक्ष को C(0, -4) पर प्रतिच्छेद करती है।

दो चरों वाले रेखीय समीकरणों का युग्म कक्षा 10 महत्वपूर्ण प्रश्न संक्षिप्त उत्तर- II (3 अंक)

प्रश्न 9.
x और y के समीकरणों के निम्नलिखित युग्म को हल कीजिए: (2012)
ए2एक्स-बी2आप= 0;ए2बीएक्स+बी2एआप= ए + बी, एक्स ≠ 0; वाई 0
समाधान:

प्रश्न 10.
x और y के लिए हल करें:
10एक्स + वाई+2एक्स - वाई= 4 ;15एक्स + वाई-5एक्स - वाई= - 2
x + y ≠ 0
x - y 0 (2012, 2017D)
हल: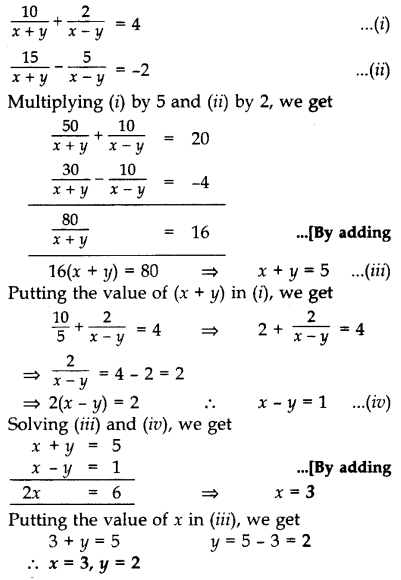

प्रश्न 11.
x और y के लिए रैखिक समीकरणों के निम्नलिखित युग्म को हल कीजिए:
141x + 93y = 189;
93x + 141y = 45 (2013)
हल:

प्रश्न 12.
x और y के रैखिक समीकरण युग्म को हल कीजिए: (2013)

bax+aby = a2 + b2; x + y = 2ab
bax+aby = a2 + b2; x + y = 2abहल:

प्रश्न 13. विलोपन द्वारा हल
करें: (2014) 3x
= y + 5
5x - y = 11 - y = 5 3(3) - y = 5 9 - 5 = y ⇒ y = 4 x = 3, y = 4

प्रश्न 14.
विलोपन द्वारा हल करें: 2015
3x - y - 7
2x + 5y + 1 = 0
हल:
3 x - y = 7 ... (i)
2x + 5y = -1 -00
समीकरण (i) को 5 और (ii) से गुणा करना ) 1 से,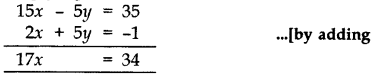

x = 2 x
के मान को (i) में रखने पर, हमारे पास
3(2)-y = 7 ⇒ 6 - 7 = y
y = -1 ∴ x = 2, y = -1

प्रश्न 15.
x और y के लिए हल करें: (2017OD)
27x + 31y = 85;
31x + 2 7y = 89
हल:

'x' का मान (i) में रखने पर हमें
2 + y = 3 y = 3 - 2 = 1
x = 2, y = 1 प्राप्त होता है।

प्रश्न 16.
x और y के लिए हल करें:एक्सए=आपबी;
ax + by = a 2 + b 2 (2017D)
हल: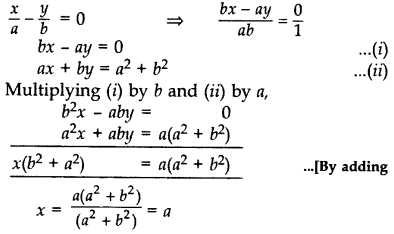

x का मान (i) में रखने पर, हमें
b(a) – ay = 0 ba = ay प्राप्त होता है।
बी एए= y b = y
x = a, y = b

प्रश्न 17.
हल करें:एक्सए+आपबी= ए + बी;एक्सए2+आपबी2=2, ए, बी ≠ 0 (2017OD)
हल: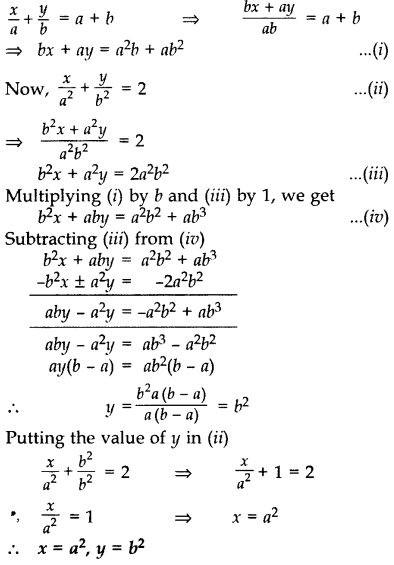

प्रश्न 18.
निम्नलिखित समीकरण युग्म को हल कीजिए: (2014)
49x + 51y = 499
51x + 49 y = 501
हल:

प्रश्न 19.
वे दो संख्याएँ ज्ञात कीजिए जिनका योग 75 और अंतर 15 है। (2014)
हल:
मान लीजिए कि दो संख्याएँ x और y हैं।
प्रश्न के अनुसार,
x + y = 75 …(i)
x – y = ±15 …(ii)
(i) और (ii) को हल करने पर, हम प्राप्त करते हैं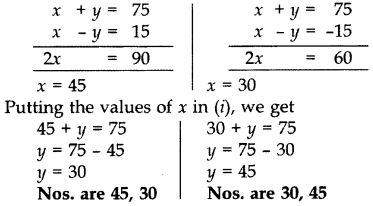

प्रश्न 20.
a और p का वह मान ज्ञात कीजिए जिसके लिए रैखिक समीकरणों के निम्नलिखित युग्म के अनंत हल हैं:
2x + 3y = 7;
αx + (α + β)y = 28 (2013)
हल:
हमारे पास 2x + 3y = 7 और αx + (α + β)y = 28 है।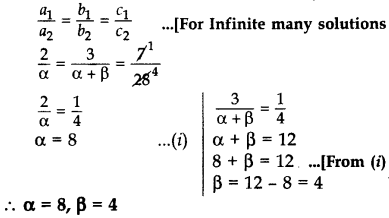

प्रश्न 21.
निम्नलिखित रैखिक समीकरण युग्म को क्रॉस गुणन विधि से हल करें: x + 2y = 2; x - 3y = 7 (2015)
हल:
x + 2y - 2 = 0
x - 3y - 7 = 0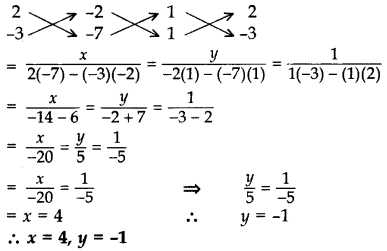

Question 22.
एक आदमी अपनी पत्नी से ₹600 प्रति माह अधिक कमाता है। आदमी के वेतन का दसवां हिस्सा और पत्नी के वेतन का एल/6 वां हिस्सा ₹1,500 है, जो हर महीने बच जाता है। उनकी आय ज्ञात कीजिए। (2014)
हल:
माना पत्नी की मासिक आय = ₹x
तो पुरुष की मासिक आय = ₹(x + 600)
प्रश्न के अनुसार,
110(एक्स + 600) +16(एक्स) = ₹1,500
3 ( एक्स + 600 ) + 5 एक्स30= ₹1,500
3x + 1,800 + 5x = ₹45,000
8x = ₹45,000 - ₹1,800
x = ₹343 , 2008= ₹5,400
पत्नी की आय = ₹x = ₹5,400
आदमी की आय = ₹(x + 600) = ₹6,000

प्रश्न 23.
दो अंकों की एक संख्या के अंकों का योग 8 है और अंकों को उलटने से बनने वाली संख्या और संख्या के बीच का अंतर 18 है। संख्या ज्ञात कीजिए। (2015)
हल:
माना इकाई और दहाई का अंक x और y है।
मूल संख्या = 1x + 10y …(i)
उलटी संख्या = 10x + 1y प्रश्नानुसार
,
x + y = 8
y = 8 - x … (ii)
साथ ही, 1x + 10Oy - (10x + y) = 18
⇒ x + 10y - 10x - y = 18
9y - 9x = 18
⇒ y - x = 2 ... [दोनों पक्षों को 9 8 से विभाजित करना
- x - x = 2 ... [से (इससे)
⇒ 8 - 2 = 2x
⇒ 2x = 6
(इसे) से, y = 8 - 3 = 5
(i) से, मूल संख्या = 3 + 10(5) = 53

दो चर वाले रैखिक समीकरणों का युग्म कक्षा 10 महत्वपूर्ण प्रश्न दीर्घ उत्तर (4 अंक)

प्रश्न 24.
पिता की आयु उसके 2 बच्चों की आयु के योग की दोगुनी है। 20 वर्ष बाद उसकी आयु उसके बच्चों की आयु के योग के बराबर होगी। पिता की आयु ज्ञात कीजिए। (2012)
हल:
माना उसके बच्चों की वर्तमान आयु x वर्ष और y वर्ष है।
तो पिता की वर्तमान आयु = 2(x + y) …(i)
20 वर्ष बाद उसके बच्चों की आयु
(x + 20) और (y + 20) वर्ष
होगी 20 वर्ष बाद पिता की आयु 2(x) होगी + y) + 20
प्रश्न के अनुसार,
2(x + y) + 20 = x + 20 + y + 20
⇒ 2x + 2y + 20 = x + y + 40
⇒ 2x + 2y - x - y = 40 - 20
⇒ x + y = 20 …[(i)
से पिता की वर्तमान आयु = 2(20) = 40 वर्ष

प्रश्न 25.
एक दो अंकों की संख्या उसके अंकों के योग का सात गुना है। अंकों को उलटने से बनने वाली संख्या दी गई संख्या से 18 कम है। दी गई संख्या ज्ञात कीजिए। (2013)
हल:
मान लीजिए इकाई के स्थान का अंक x और दहाई के स्थान का अंक bey है।
तब मूल संख्या = x + 10y
और उलटी संख्या = 10x + y
प्रश्न के अनुसार,
x + 10y = 7(x + y)
x + 10y = 7x + 7y
10y - 7y = 7x - x
3y = 6x y = 2x ...(i)
(x + 10y) - (10x + y) = 18
x + 10y - 10x - y = 18
9y - 9x = 180
y - x = 2 ... [9
2x - x = से भाग देने पर = 2 ...[(i)
x = 2
से 'x' का मान (i) रखने पर हमें y = 2(2) = 4 प्राप्त होता है।
अभीष्ट संख्या = x + 10y
= 2 + 10(4) = 42

Question 26.
सीता देवी गली के जानवरों को पीने का पानी उपलब्ध कराने के उद्देश्य से सड़क के किनारे एक आयताकार तालाब बनाना चाहती हैं। यदि तालाब की लंबाई 2 फीट कम और चौड़ाई 1 फीट बढ़ा दी जाए तो तालाब का क्षेत्रफल 3 वर्ग फीट कम हो जाएगा। लंबाई 1 फीट बढ़ा दी जाए और चौड़ाई शेष रह जाए तो इसका क्षेत्रफल 4 वर्ग फीट बढ़ जाएगा। वही। तालाब के आयामों का पता लगाएं। (2014)
हल:
माना आयताकार तालाब की लंबाई = x
और आयताकार तालाब की चौड़ाई = y
आयताकार तालाब का क्षेत्रफल = xy
प्रश्न के अनुसार,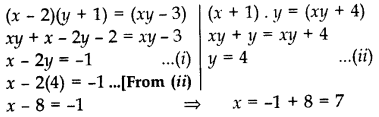

आयताकार तालाब की लंबाई = 7 फीट।
आयताकार तालाब की चौड़ाई = 4 फीट।

प्रश्न 27.
दो अंकों की एक संख्या के अंकों को उलटने पर प्राप्त संख्या मूल संख्या के तीन गुने से 9 कम होती है। यदि इन दोनों संख्याओं का अंतर 45 है, तो मूल संख्या ज्ञात कीजिए। (2014)
हल:
मान लीजिए इकाई के स्थान का अंक x और दहाई के स्थान का अंक bey है।
मूल संख्या = x + 10y उलटी संख्या = 10x + y
प्रश्न के अनुसार,
10x + y = 3(x + 10y) - 9
⇒ 10x + y = 3x + 30y - 9
10x + y - 3x - 30y = - 9
7x - 29y = -9 ... (i)
10x + y - (x + 10y) = 45
⇒ 9x - 9y = 45
⇒ x - y = 5 ... [दोनों पक्षों को 9
x - 5 + y …( ii)
हल करना (i),
7x - 29y = -9
7(5 + y) - 29y = -9 …[(ii)
35+ 7y - 29y = -9 से
-22y = -9 - 35
-22y = -44 ⇒ y =4422= 2
y के मान को (ii) में रखने पर,
x = 5 + 2 = 7
मूल संख्या = x + 10y
= 7 + 10(2) = 27

Question 28. शांत
जल में एक नाव की गति 15 किमी/घंटा है। यह धारा के प्रतिकूल 30 किमी जाती है और 4 घंटे 30 मिनट में उसी बिंदु पर वापस आती है। धारा की गति ज्ञात कीजिए। 2017D
हल: माना
धारा की गति = x किमी/घंटा शांत
पानी में नाव की गति = 15 किमी/घंटा
तो, धारा के प्रतिकूल नाव की गति = (15 - x) किमी/घंटा
और नाव की गति धारा के अनुकूल = (15 + x) किमी/घंटा

धारा की गति = 5 किमी/घंटा

Question 29.
एक टैक्सी कंपनी का मालिक सभी टैक्सियों को पेट्रोल/डीजल के बजाय सीएनजी ईंधन पर चलाने का फैसला करता है। शहर में टैक्सी शुल्क में तय की गई दूरी के लिए शुल्क के साथ-साथ निर्धारित शुल्क शामिल हैं। 12 किमी की यात्रा के लिए भुगतान किया गया शुल्क 789 है और 20 किमी की यात्रा के लिए भुगतान किया गया शुल्क ₹145 है।
एक व्यक्ति को 30 किमी की दूरी तय करने के लिए क्या भुगतान करना होगा? (2014)
हल: माना
स्थिर शुल्क = 7x
और प्रति किमी शुल्क = ₹y
प्रश्न के अनुसार,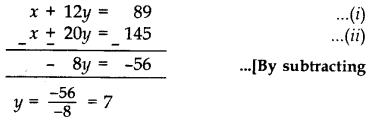

y के मान को (i) में रखने पर, हमें
x + 12 (7) = 89
x + 84 = 89 मिलता है। x = 89 - 84 = 5
30 किमी का कुल किराया = x + 30y = 5 + 30 (7)
= 5 + 210 = ₹215

प्रश्न 30.
एक नाव धारा के अनुकूल 44 किमी जाने में 4 घंटे का समय लेती है और उतनी ही समय में वह 20 किमी धारा के प्रतिकूल जा सकती है। शांत जल में धारा और नाव की गति ज्ञात कीजिए। (2015)
हल:
माना धारा की गति = y किमी/घंटा
मान लीजिए शांत पानी में नाव की गति = x किमी/घंटा
है, तो धारा के अनुकूल नाव की गति = (x + y) किमी/घंटा
और, धारा के प्रतिकूल नाव की गति = (x - y) किमी / घंटा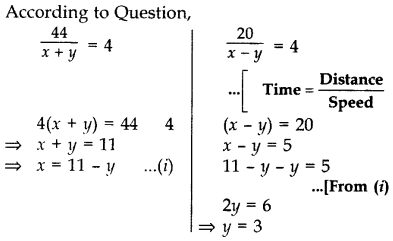

(i) से, x = 11 - 3 = 8
धारा की गति, y = 3 किमी / घंटा
शांत पानी में नाव की गति, x = 8 किमी/घंटा

Question 31.
एक आदमी 300 किमी की यात्रा आंशिक रूप से ट्रेन से और आंशिक रूप से कार से करता है। यदि वह 60 किमी ट्रेन से और बाकी कार से यात्रा करता है तो उसे 4 घंटे लगते हैं। यदि वह 100 किमी ट्रेन से और शेष कार द्वारा यात्रा करता है, तो उसे 10 मिनट अधिक समय लगता है। ट्रेन और कार की गति अलग-अलग ज्ञात कीजिए। (2017D)
हल:
माना ट्रेन की गति = x किमी/घंटा
मान लीजिए कार की गति = y किमी/घंटा
प्रश्न के अनुसार,

ट्रेन की गति = 60 किमी/घंटा
और कार की गति = 80 kn / घंटा

Question 32.
एक टैक्सी कंपनी का मालिक सभी टैक्सियों को पेट्रोल/डीजल के बजाय सीएनजी ईंधन पर चलाने का फैसला करता है। शहर में टैक्सी शुल्क में तय की गई दूरी के लिए शुल्क के साथ-साथ निर्धारित शुल्क शामिल हैं। 13 किमी की यात्रा के लिए भुगतान किया गया शुल्क ₹129 है और 22 किमी की यात्रा के लिए भुगतान किया गया शुल्क ₹210 है।
32 किमी की दूरी तय करने के लिए एक व्यक्ति को क्या भुगतान करना होगा? (2014)
हल:
मान लीजिए कि नियत शुल्क ₹x है और दूरी के लिए शुल्क = ₹y प्रति किमी
प्रश्न के अनुसार,
13 किमी की यात्रा के लिए,
x + 13y = 129 x = 129 - 13y …(/)
के लिए 22 किमी की यात्रा, x + 22y = 210 ... (ii)
129 - 13y + 22y = 210 ... [से (i)
9y = 210 - 129 = 81
9y = 81 ⇒ y = 9
से (i), x = 129 - 13(9)
= 129 - 117 = 12
फिक्स्ड चार्ज, x = ₹12
दूरी के लिए चार्ज, y = ₹9 प्रति किमी
32 किमी की दूरी की यात्रा के लिए भुगतान करने के लिए
= x + 32y = 12 + 32(9) = 12 + 288 = ₹300

प्रश्न 33.
रैखिक समीकरणों के निम्नलिखित युग्म को आलेखीय रूप से हल कीजिए:
x + 3y = 6; 2x - 3y = 12
दिए गए समीकरणों को y-अक्ष से निरूपित करने वाली रेखाओं से बने त्रिभुज का क्षेत्रफल भी ज्ञात कीजिए। (2012, 2015)
हल: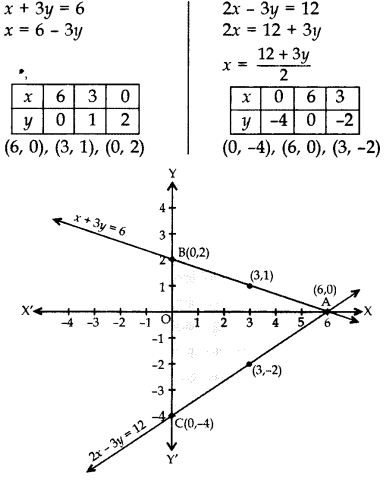

बिंदुओं को प्लॉट करके और उन्हें जोड़कर, रेखाएँ A(6, 0)
∴ x = 6, y = 0
पर प्रतिच्छेद करती हैं रेखा x + 3y = 6, Y-अक्ष को B(0, 2) पर काटती हैं और रेखा 2x - 3y = 12, Y-अक्ष को C(0, -4) पर काटती है। अत: y-अक्ष वाली रेखाओं से बने त्रिभुज का क्षेत्रफल।
त्रिभुज का क्षेत्रफल
=12× आधार × संगत ऊँचाई
=12× ईसा पूर्व × एओ =12× 6 × 6 = 18 वर्ग इकाई

प्रश्न 34.
निम्नलिखित समीकरणों के आलेख खींचिए:
2x - y = 1; x + 2y = 13
ग्राफ से समीकरणों का हल ज्ञात कीजिए और रेखाओं और y-अक्ष से बने त्रिभुजाकार क्षेत्र को छायांकित कीजिए। (2013)
हल: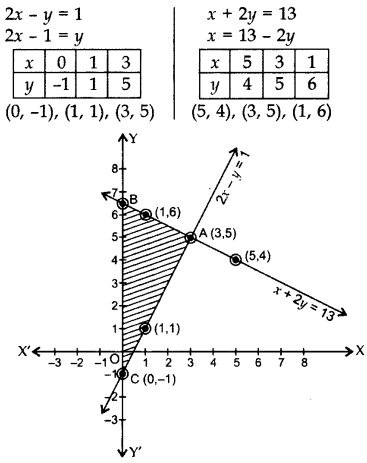

बिन्दुओं को आलेखित करके और उन्हें मिलाने से, रेखाएँ A(3,5) पर प्रतिच्छेद करती हैं।
x = 3, y = 5
यहाँ ABC अभीष्ट त्रिभुज है।

प्रश्न 35.
समीकरण x - y + 1 = 0 और 3x + 2y - 12 = 0 के आलेख खींचिए। इन रेखाओं और x-अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए। (2012, 2017D)
हल: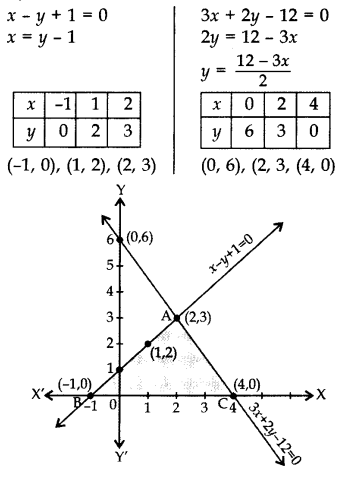

रेखाएं (2, 3)
x = 2, y = 3
पर प्रतिच्छेद करती हैं, ABC के शीर्ष A(2, 3), B(-1, 0) और C(4, 0) हैं।

Question 36.
अमित ने ₹11 में दो पेंसिल और तीन चॉकलेट खरीदी और सुमीत ने ₹7 में एक पेंसिल और दो चॉकलेट खरीदी। इस स्थिति को रैखिक समीकरणों के युग्म के रूप में निरूपित करें। एक पेंसिल और एक चॉकलेट की कीमत आलेखीय रूप से ज्ञात कीजिए। (2017OD)
हल:
माना एक पेंसिल की कीमत = ₹x और एक चॉकलेट की कीमत = ₹y.
प्रश्न के अनुसार,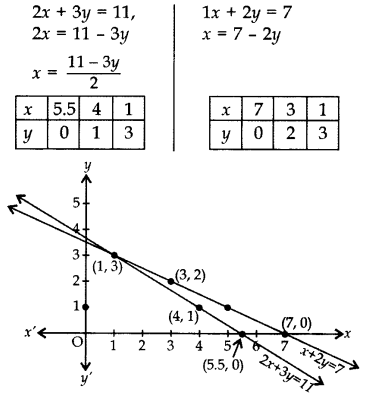

रेखाएँ (1, 3) पर प्रतिच्छेद करती हैं।
x = 1, y = 3
इसलिए एक पेंसिल का मूल्य = ₹1 और एक चॉकलेट का मूल्य = ₹3

प्रश्न 37.
7x - 5y - 4 = 0 दिया गया है। एक अन्य रैखिक समीकरण लिखिए, जिससे कि युग्म द्वारा निरूपित रेखाएँ इस प्रकार हों:
(i) प्रतिच्छेद
(ii) संपाती
(iii) समानांतर (2015 OD)
हल:
7x - 5y - 4 = 0