कक्षा 10 गणित अध्याय 5 के लिए एनसीईआरटी समाधान
कक्षा 10 गणित अध्याय 5 समान्तर श्रेणी के लिए एनसीईआरटी समाधान सीबीएसई टर्म II कक्षा 10 गणित परीक्षा की तैयारी कर रहे छात्रों के लाभ के लिए यहां प्रस्तुत किया गया है। कक्षा 10 की परीक्षा में अच्छे अंक प्राप्त करने के लिए छात्रों को एनसीईआरटी के इन समाधानों से अच्छी तरह वाकिफ होना बहुत जरूरी है । इन NCERT समस्याओं का समाधान BYJU'S के विशेषज्ञों द्वारा किया जाता है। ये समाधान आपको अंकगणितीय प्रगति पर विभिन्न प्रकार के प्रश्नों को समझने और उनमें महारत हासिल करने में मदद करेंगे। एनसीईआरटी समाधान आपको विभिन्न प्रकार के प्रश्नों को हल करने में पूर्णता प्राप्त करने में मदद करते हैं।
कक्षा 10 के लिए गणित एनसीईआरटी समाधान के उत्तर अध्याय 5 - समान्तर श्रेणी
Exercise - 5.1 पृष्ठ: 99
1. निम्नलिखित में से किस स्थिति में शामिल संख्याओं की सूची अंकगणितीय प्रगति के रूप में बनती है और क्यों?
(i) प्रत्येक किमी के बाद टैक्सी का किराया जब पहले किमी के लिए किराया 15 रुपये और प्रत्येक अतिरिक्त किमी के लिए 8 रुपये है।
समाधान:
हम दी गई शर्त को इस प्रकार लिख सकते हैं;
1 किमी = 15 . के लिए टैक्सी का किराया
पहले 2 किलोमीटर के लिए टैक्सी का किराया = 15+8 = 23
पहले 3 किलोमीटर के लिए टैक्सी का किराया = 23+8 = 31
पहले 4 किलोमीटर के लिए टैक्सी का किराया = 31+8 = 39
और इसी तरह……
इस प्रकार, 15, 23, 31, 39 ... एक AP बनाता है क्योंकि प्रत्येक अगला पद पिछले पद से 8 अधिक है।
(ii) एक सिलेंडर में मौजूद हवा की मात्रा जब एक वैक्यूम पंप एक बार में सिलेंडर में शेष हवा का 1/4 भाग निकाल देता है।
समाधान:
मान लीजिए कि एक बेलन में वायु का आयतन प्रारंभ में V लीटर है।
प्रत्येक स्ट्रोक में, वैक्यूम पंप एक बार में सिलेंडर में शेष हवा का 1/4 भाग निकाल देता है। या हम कह सकते हैं, हर झटके के बाद हवा का 1-1/4 = 3/4 भाग रह जाएगा।
इसलिए, वॉल्यूम V , 3 V /4 , (3 V /4) 2 , (3 V / 4) 3 … और इसी तरह होंगे
स्पष्ट रूप से, हम यहाँ देख सकते हैं, इस श्रृंखला के आसन्न पदों में उनके बीच सामान्य अंतर नहीं है। अत: यह श्रंखला एक AP नहीं है
(iii) प्रत्येक मीटर खुदाई के बाद एक कुआँ खोदने की लागत, जब पहले मीटर के लिए 150 रुपये की लागत आती है और बाद में प्रत्येक मीटर के लिए 50 रुपये बढ़ जाती है।
समाधान:
हम दी गई शर्त को इस प्रकार लिख सकते हैं;
पहले मीटर के लिए कुआँ खोदने का खर्च = 150 रुपये
पहले 2 मीटर के लिए एक कुआँ खोदने की लागत = रु.150+50 = रु.200
पहले 3 मीटर के लिए एक कुआँ खोदने की लागत = रु.200+50 = रु.250
पहले 4 मीटर के लिए एक कुआँ खोदने की लागत = 250 रुपये + 50 = 300 रुपये
और इसी तरह..
स्पष्ट रूप से, 150, 200, 250, 300 ... प्रत्येक पद के बीच 50 के सामान्य अंतर के साथ एक AP बनाता है।
(iv) खाते में प्रति वर्ष वह राशि, जब 8% वार्षिक की दर से चक्रवृद्धि ब्याज पर 10000 रुपये जमा किए जाते हैं।
समाधान:
हम जानते हैं कि यदि रु. P को n वर्षों के लिए r % चक्रवृद्धि ब्याज पर प्रतिवर्ष जमा किया जाता है, धन की राशि होगी:
पी(1+आर/100) एन
इसलिए, प्रत्येक वर्ष के बाद, राशि होगी;
10000(1+8/100), 10000(1+8/100) 2 , 10000(1+8/100) 3 ……
स्पष्ट रूप से, इस श्रृंखला के पदों में उनके बीच सामान्य अंतर नहीं है। इसलिए, यह एक AP . नहीं है
2. AP के पहले चार पद लिखिए जब पहला पद a और सार्व अंतर इस प्रकार दिया गया हो :
(i) a = 10, d = 10
(ii) a = -2, d = 0
(iii) a = 4, d =
-3 (iv) a = -1 d = 1/2
(v) a = - 1.25, घ = - 0.25
समाधान:
(i) ए = 10, डी = 10
आइए मान लें, अंकगणितीय प्रगति श्रृंखला एक 1 , ए 2 , ए 3 , ए 4 , ए 5 ...
ए 1 = ए = 10
ए 2 = ए 1 + डी = 10+10 = 20
ए 3 = ए 2 + डी = 20 + 10 = 30
ए 4 = ए 3 + डी = 30 + 10 = 40
ए 5 = ए 4 + डी = 40 + 10 = 50
और इसी तरह…
अत: AP श्रंखला 10, 20, 30, 40, 50...
और इस AP के पहले चार पद 10, 20, 30 और 40 होंगे।
(ii) ए = - 2, डी = 0
आइए मान लें, अंकगणितीय प्रगति श्रृंखला एक 1 , ए 2 , ए 3 , ए 4 , ए 5 ...
ए 1 = ए = -2
ए 2 = ए 1 + डी = - 2+0 = - 2
ए 3 = ए 2 + डी = - 2+0 = - 2
ए 4 = ए 3 + डी = - 2 + 0 = - 2
अत: AP श्रंखला – 2, – 2, – 2, – 2…
और, इस AP के पहले चार पद होंगे - 2, - 2, - 2 और - 2।
(iii) ए = 4, डी = - 3
आइए मान लें, अंकगणितीय प्रगति श्रृंखला एक 1 , ए 2 , ए 3 , ए 4 , ए 5 ...
ए 1 = ए = 4
ए 2 = ए 1 + डी = 4-3 = 1
ए 3 = ए 2 + डी = 1-3 = - 2
ए 4 = ए 3 + डी = -2-3 = - 5
अत: AP श्रंखला 4, 1, – 2 – 5…
और, इस AP के पहले चार पद 4, 1, - 2 और - 5 होंगे।
(iv) ए = - 1, डी = 1/2
आइए मान लें, अंकगणितीय प्रगति श्रृंखला एक 1 , ए 2 , ए 3 , ए 4 , ए 5 ...
ए 2 = ए 1 + डी = -1+1/2 = -1/2
ए 3 = ए 2 + डी = -1/2+1/2 = 0
ए 4 = ए 3 + डी = 0+1/2 = 1/2
इस प्रकार, AP श्रृंखला होगी-1, -1/2, 0, 1/2
और इस AP के पहले चार पद -1, -1/2, 0 और 1/2 होंगे।
(v) ए = - 1.25, डी = - 0.25
आइए मान लें, अंकगणितीय प्रगति श्रृंखला एक 1 , ए 2 , ए 3 , ए 4 , ए 5 ...
ए 1 = ए = - 1.25
ए 2 = ए 1 + डी = - 1.25-0.25 = - 1.50
ए 3 = ए 2 + डी = - 1.50 - 0.25 = - 1.75
ए 4 = ए 3 + डी = - 1.75 - 0.25 = - 2.00
अत: AP श्रंखला 1.25, – 1.50, – 1.75, – 2.00 …….. होगी।
और इस AP के पहले चार पद होंगे - 1.25, - 1.50, - 1.75 और - 2.00।
3. निम्नलिखित APs के लिए पहला पद और सार्व अंतर लिखिए।
(i) 3, 1, - 1, - 3 ...
(ii) -5, - 1, 3, 7 ...
(iii) 1/3, 5/3, 9/3, 13/3…।
(iv) 0.6, 1.7, 2.8, 3.9 ...
समाधान
(i) दी गई श्रृंखला,
3, 1, - 1, - 3 ...
पहला पद, a = 3
उभयनिष्ठ अंतर, d = दूसरा पद – पहला पद
1 - 3 = -2
डी = -2
(ii) दी गई श्रृंखला, – 5, – 1, 3, 7…
पहला पद, a = -5
उभयनिष्ठ अंतर, d = दूसरा पद – पहला पद
(-1)-( – 5) = - 1+5 = 4
(iii) दी गई श्रृंखला, 1/3, 5/3, 9/3, 13/3…।
पहला पद, a = 1/3
उभयनिष्ठ अंतर, d = दूसरा पद – पहला पद
5/3 - 1/3 = 4/3
(iv) दी गई श्रृंखला, 0.6, 1.7, 2.8, 3.9 ...
पहला पद, a = 0.6
उभयनिष्ठ अंतर, d = दूसरा पद – पहला पद
1.7 - 0.6
1.1
4. निम्नलिखित में से कौन एपी हैं? यदि वे एक AP बनाते हैं तो सार्व अंतर d ज्ञात कीजिए और तीन और पद लिखिए।
(i) 2, 4, 8, 16
(ii) 2, 5/2, 3, 7/2।
(iii) -1.2, -3.2, -5.2, -7.2
(iv) -10, -6, -2, 2…
(v) 3, 3 + √2, 3 + 2√2, 3 + 3√2
( vi) 0.2, 0.22, 0.222, 0.2222।
(vii) 0,
-4, -8, -12 (viii) -1/2, -1/2, -1/2, -1/2।
(ix) 1, 3, 9, 27…
(x) a , 2 a , 3 a , 4 a …
(xi) a , a 2 , a 3 , a 4 …
(xii) 2, √8, √18 , √32…
(xiii) 3, √6, 9, √12…
(xiv) 1 2 , 3 2 , 5 2 , 72 ...
(xv) 1 2 , 5 2 , 7 2 , 7 3 ...
समाधान
(i) हमें दिया गया,
2, 4, 8, 16…
यहाँ, सामान्य अंतर है;
ए 2 - ए 1 = 4 - 2 = 2
ए 3 - ए 2 = 8 - 4 = 4
ए 4 - ए 3 = 16 - 8 = 8
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान नहीं होता है।
इसलिए, दी गई श्रृंखला AP नहीं बना रही है
(ii) दिया गया है, 2, 5/2, 3, 7/2….
यहां,
ए 2 - ए 1 = 5/2-2 = 1/2
ए 3 - ए 2 = 3-5/2 = 1/2
ए 4 - ए 3 = 7/2-3 = 1/2
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान होता है।
इसलिए, d = 1/2 और दी गई श्रृंखला AP . में हैं
अगले तीन पद हैं;
ए 5 = 7/2+1/2 = 4
और 6 = 4 +1/2 = 9/2
ए 7 = 9/2 +1/2 = 5
(iii) दिया गया है, -1.2, - 3.2, -5.2, -7.2 ...
यहां,
ए 2 - ए 1 = (-3.2)-(-1.2) = -2
ए 3 - ए 2 = (-5.2)-(-3.2) = -2
ए 4 - ए 3 = (-7.2)-(-5.2) = -2
चूँकि, n +1 – a n या सार्व अंतर हर बार समान होता है ।
इसलिए, d = -2 और दी गई श्रृंखला AP . में हैं
अत: अगले तीन पद हैं;
ए 5 = - 7.2-2 = -9.2
और 6 = - 9.2-2 = - 11.2
ए 7 = - 11.2-2 = - 13.2
(iv) दिया गया है, -10, - 6, - 2, 2 ...
यहाँ, पद और उनके अंतर हैं;
ए 2 - ए 1 = (-6)-(-10) = 4
ए 3 - ए 2 = (-2)-(-6) = 4
ए 4 - ए 3 = (2 -(-2) = 4
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान होता है।
इसलिए, d = 4 और दी गई संख्याएँ AP . में हैं
अत: अगले तीन पद हैं;
ए 5 = 2+4 = 6
और 6 = 6 + 4 = 10
ए 7 = 10 + 4 = 14
(v) दिया गया है, 3, 3+√2, 3+2√2, 3+3√2
यहाँ,
ए 2 - ए 1 = 3+√2-3 = √2
ए 3 - ए 2 = (3+2√2)-(3+√2) = √2
ए 4 - ए 3 = (3+3√2) - (3+2√2) = √2
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान होता है।
इसलिए, d = 2 और दी गई श्रृंखला एक AP बनाती है
अत: अगले तीन पद हैं;
ए 5 = (3+√2) +√2 = 3+4√2
और 6 = (3 + 4√2) + √2 = 3 + 5√2
ए 7 = (3+5√2)+√2 = 3+6√2
(vi) 0.2, 0.22, 0.222, 0.2222….
यहां,
ए 2 - ए 1 = 0.22-0.2 = 0.02
ए 3 - ए 2 = 0.222 - 0.22 = 0.002
ए 4 - ए 3 = 0.2222-0.222 = 0.0002
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान नहीं होता है।
इसलिए, और दी गई श्रृंखला AP नहीं बनाती है
(vii) 0, -4, -8, -12 ...
यहां,
ए 2 - ए 1 = (-4)-0 = -4
ए 3 - ए 2 = (-8)-(-4) = -4
ए 4 - ए 3 = (-12)-(-8) = -4
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान होता है।
इसलिए, d = -4 और दी गई श्रृंखला एक AP बनाती है
अत: अगले तीन पद हैं;
ए 5 = -12-4 = -16
और 6 = -16-4 = -20
ए 7 = -20-4 = -24
(viii) -1/2, -1/2, -1/2, -1/2 ….
यहां,
ए 2 - ए 1 = (-1/2) - (-1/2) = 0
ए 3 - ए 2 = (-1/2) - (-1/2) = 0
ए 4 - ए 3 = (-1/2) - (-1/2) = 0
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान होता है।
इसलिए, d = 0 और दी गई श्रृंखला एक AP बनाती है
अत: अगले तीन पद हैं;
ए 5 = (-1/2)-0 = -1/2
और 6 = (-1/2) -0 = -1/2
ए 7 = (-1/2)-0 = -1/2
(ix) 1, 3, 9, 27…
यहाँ,
ए 2 - ए 1 = 3-1 = 2
ए 3 - ए 2 = 9-3 = 6
ए 4 - ए 3 = 27-9 = 18
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान नहीं होता है।
इसलिए, और दी गई श्रृंखला AP नहीं बनाती है
(एक्स) ए , 2 ए , 3 ए , 4 ए …
यहां,
ए 2 - ए 1 = 2 ए - ए = ए
ए 3 - ए 2 = 3 ए -2 ए = ए
ए 4 - ए 3 = 4 ए -3 ए = ए
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान होता है।
इसलिए, d = a और दी गई श्रृंखला एक AP बनाती है
अत: अगले तीन पद हैं;
ए 5 = 4 ए + ए = 5 ए
ए 6 = 5 ए + ए = 6 ए
ए 7 = 6 ए + ए = 7 ए
(xi) ए , ए 2 , ए 3 , ए 4 …
यहां,
ए 2 - ए 1 = ए 2 - ए = ए ( ए -1)
ए 3 - ए 2 = ए 3 - ए 2 = ए 2 ( ए -1)
ए 4 - ए 3 = ए 4 - ए 3 = ए 3 ( ए -1)
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान नहीं होता है।
इसलिए, दी गई श्रृंखला AP नहीं बनाती है
(xii) 2, √8, √18, 32 ...
यहाँ,
ए 2 - ए 1 = √8-√2 = 2√2-√2 = √2
ए 3 - ए 2 = √18-√8 = 3√2-2√2 = √2
ए 4 - ए 3 = 4√2-3√2 = √2
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान होता है।
इसलिए, d = 2 और दी गई श्रृंखला एक AP बनाती है
अत: अगले तीन पद हैं;
एक 5 = √32+√2 = 4√2+√2 = 5√2 = √50
और 6 = 5√2 + √2 = 6√2 = √72
एक 7 = 6√2+√2 = 7√2 = √98
(xiii) 3, 6, 9, 12 ...
यहां,
ए 2 - ए 1 = √6-√3 = √3×√2-√3 = √3 (√2-1)
ए 3 - ए 2 = √9-√6 = 3-√6 = √3 (√3-√2)
ए 4 - ए 3 = √12 - √9 = 2√3 - √3 × √3 = √3 (2-√3)
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान नहीं होता है।
इसलिए, दी गई श्रृंखला AP नहीं बनाती है
(xiv) 1 2 , 3 2 , 5 2 , 7 2 …
या, 1, 9, 25, 49…..
यहां,
ए 2 - ए 1 = 9−1 = 8
ए 3 - ए 2 = 25−9 = 16
a 4 - a 3 = 49−25 = 24
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान नहीं होता है।
इसलिए, दी गई श्रृंखला AP नहीं बनाती है
(xv) 1 2 , 5 2 , 7 2 , 73 …
या 1, 25, 49, 73...
यहां,
ए 2 - ए 1 = 25−1 = 24
ए 3 - ए 2 = 49−25 = 24
ए 4 - ए 3 = 73−49 = 24
चूँकि, a n +1 – a n या सार्व अंतर हर बार समान होता है।
इसलिए, d = 24 और दी गई श्रृंखला एक AP बनाती है
अत: अगले तीन पद हैं;
ए 5 = 73+24 = 97
और 6 = 97 + 24 = 121
ए 7 = 121 + 24 = 145
Exercise - 5.2 पृष्ठ: 105
1. निम्नलिखित तालिका में रिक्त स्थानों की पूर्ति करें, यह देखते हुए कि a पहला पद है, d सामान्य अंतर है और AP का n वाँ पद है
समाधान:
(i) दिया गया,
पहला पद, a = 7
सामान्य अंतर, डी = 3
पदों की संख्या, n = 8,
हमें nवाँ पद ज्ञात करना है, a n = ?
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
मान डालते हैं,
=> 7+(8 −1) 3
=> 7+(7) 3
=> 7+21 = 28
इसलिए, एक n = 28
(ii) दिया गया,
पहला पद, a = -18
सामान्य अंतर, d = ?
पदों की संख्या, n = 10
वां पद, एक n = 0
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
मान डालते हैं,
0 = - 18 +(10−1) डी
18 = 9 डी
डी = 18/9 = 2
अत: सार्व अंतर, d = 2
(iii) दिया गया,
पहला पद, a = ?
सामान्य अंतर, डी = -3
पदों की संख्या, n = 18
वां पद, एक n = -5
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
मान डालते हैं,
−5 = ए +(18−1) (−3)
−5 = ए +(17) (−3)
−5 = एक −51
ए = 51−5 = 46
अत: a = 46
(iv) दिया गया,
पहला पद, a = -18.9
सामान्य अंतर, डी = 2.5
पदों की संख्या, n = ?
वां पद, एक n = 3.6
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
मान डालते हैं,
3.6 = - 18.9+( एन -1)2.5
3.6 + 18.9 = ( एन -1)2.5
22.5 = ( एन -1)2.5
( एन -1) = 22.5/2.5
एन - 1 = 9
एन = 10
इसलिए, n = 10
(v) दिया गया,
पहला पद, a = 3.5
सामान्य अंतर, डी = 0
पदों की संख्या, n = 105
वां पद, एक n = ?
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
मान डालते हैं,
एक एन = 3.5+(105−1) 0
एक एन = 3.5+104×0
एक एन = 3.5
इसलिए, एक n = 3.5
2. निम्नलिखित में से सही विकल्प चुनें और औचित्य सिद्ध करें:
(i) एपी का 30 वां पद: 10,7, 4, ..., है
(ए) 97 (बी) 77 (सी) -77 (डी) -87
(ii) AP -3, -1/2, ,2… का 11 वाँ पद। है
(ए) 28 (बी) 22 (सी) - 38 (डी)
समाधान:
(i) यहां दिया गया है,
एपी = 10, 7, 4,…
इसलिए, हम पा सकते हैं,
पहला पद, a = 10
सामान्य अंतर, d = a 2 - a 1 = 7−10 = -3
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
मान डालना;
एक 30 = 10+(30−1)(−3)
ए 30 = 10+(29)(−3)
एक 30 = 10−87 = −77
अत: सही उत्तर विकल्प सी है।
(ii) यहां दिया गया है,
एपी = -3, -1/2, ,2 …
इसलिए, हम पा सकते हैं,
पहला पद a = - 3
सामान्य अंतर, d = a 2 - a 1 = (-1/2) -(-3)
(-1/2) + 3 = 5/2
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
मान डालना;
ए 11 = -3+ (11-1) (5/2)
ए 11 = -3+ (10) (5/2)
ए 11 = -3 + 25
एक 11 = 22
अतः उत्तर विकल्प B है।
3. निम्नलिखित AP में बक्सों में लुप्त पद ज्ञात कीजिए।
समाधान:
(i) दिए गए AP के लिए, 2,2 , 26
पहला और तीसरा पद हैं;
ए = 2
ए 3 = 26
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
इसलिए, मूल्यों को यहाँ रखते हुए,
ए 3 = 2+(3-1) डी
26 = 2+ 2d
24 = 2d
डी = 12
ए 2 = 2+(2-1)12
= 14
अत: 14 लुप्त पद है।
(ii) दिए गए एपी के लिए, 13, ,3
ए 2 = 13 और
ए 4 = 3
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
इसलिए, मूल्यों को यहाँ रखते हुए,
ए 2 = ए + (2-1) डी
13 = ए + डी ………………। (मैं)
ए 4 = ए + (4-1) डी
3 = ए +3 डी …………… .. (ii)
समीकरण (i) को (ii) से घटाने पर , हम प्राप्त करते हैं,
- 10 = 2d
डी = - 5
समीकरण (i) से, d का मान रखने पर, हमें प्राप्त होता है
13 = ए +(-5)
ए = 18
ए 3 = 18+ (3-1) (- 5)
= 18+2(-5) = 18-10 = 8
अत: लुप्त पद क्रमशः 18 और 8 हैं।
(iii) दिए गए एपी के लिए,
ए = 5 और
a4 = 19/2
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
इसलिए, मूल्यों को यहाँ रखते हुए,
ए 4 = ए + (4-1) डी
19/2 = 5 +3d
(19/2) - 5 = 3डी
3डी = 9/2
डी = 3/2
ए 2 = ए + (2-1) डी
ए 2 = 5 +3/2
ए 2 = 13/2
ए 3 = ए + (3-1) डी
और 3 = 5 + 2 × 3/2
ए 3 = 8
अत: लुप्त पद क्रमशः 13/2 और 8 हैं।
(iv) दिए गए एपी के लिए,
ए = -4 और
और 6 = 6
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
इसलिए, मूल्यों को यहाँ रखते हुए,
ए 6 = ए + (6−1) डी
6 = - 4+5 डी
10 = 5 डी
डी = 2
ए 2 = ए + डी = -4+2 = -2
ए 3 = ए +2 डी = -4+2(2) = 0
a 4 = a +3 d = − 4+ 3(2) = 2
a 5 = a +4 d = − 4+4(2) = 4
अतः लुप्त पद क्रमशः -2, 0, 2 और 4 हैं।
(v) दिए गए एपी के लिए,
ए 2 = 38
एक 6 = −22
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
इसलिए, मूल्यों को यहाँ रखते हुए,
ए 2 = ए +(2−1) डी
38 = ए + डी ………………। (मैं)
ए 6 = ए + (6−1) डी
−22 = ए +5 डी …………………। (ii)
समीकरण (i) को (ii) से घटाने पर , हम प्राप्त करते हैं
- 22 - 38 = 4 डी
−60 = 4 डी
डी = -15
ए = ए 2 - डी = 38 - (−15) = 53
ए 3 = ए + 2 डी = 53 + 2 (−15) = 23
ए 4 = ए + 3 डी = 53 + 3 (−15) = 8
a 5 = a + 4 d = 53 + 4 (−15) = −7
अतः लुप्त पद क्रमशः 53, 23, 8 और -7 हैं।
4. एपी 3, 8, 13, 18, … का कौन सा पद 78 है?
समाधान:
AP श्रंखला को 3, 8, 13, 18,…
पहला पद, a = 3
सामान्य अंतर, d = a 2 - a 1 = 8 - 3 = 5
मान लीजिए दिए गए AP का n वाँ पद 78 है। अब जैसा कि हम जानते हैं,
ए एन = ए +( एन -1) डी
इसलिए,
78 = 3+( एन −1)5
75 = ( एन -1)5
( एन -1) = 15
एन = 16
अत: इस AP का 16 वाँ पद 78 है।
5. निम्नलिखित AP में से प्रत्येक में पदों की संख्या ज्ञात कीजिए
(i) 7, 13, 19, …, 205
समाधान:
(i) दिया गया है, 7, 13, 19, …, 205 AP . है
इसलिए
पहला पद, a = 7
सामान्य अंतर, d = a 2 - a 1 = 13 - 7 = 6
माना इस AP में n पद हैं
एक एन = 205
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए + ( एन -1) डी
इसलिए, 205 = 7 + ( एन -1) 6
198 = ( एन -1) 6
33 = ( एन -1)
एन = 34
अत: इस दी गई श्रंखला में 34 पद हैं।
पहला पद, a = 18
सामान्य अंतर, d = a 2 -a 1 =
डी = (31-36)/2 = -5/2
माना इस AP में n पद हैं
एक एन = -47
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए+(एन−1)डी
-47 = 18+(n-1)(-5/2)
-47-18 = (एन -1) (-5/2)
-65 = (एन -1) (-5/2)
(एन-1) = -130/-5
(एन -1) = 26
एन = 27
इसलिए, इस दिए गए AP में 27 पद हैं।
6. जाँच कीजिए कि क्या -150 AP 11, 8, 5, 2,… का एक पद है।
समाधान:
दी गई श्रृंखला के लिए, एपी 11, 8, 5, 2।
पहला पद, a = 11
सामान्य अंतर, d = a 2 - a 1 = 8−11 = −3
माना −150 इस AP का n वाँ पद है
जैसा कि हम जानते हैं, एक एपी के लिए,
ए एन = ए +( एन -1) डी
-150 = 11+( एन -1)(-3)
-150 = 11-3 एन +3
-164 = -3 एन
एन = 164/3
स्पष्ट रूप से, n एक पूर्णांक नहीं बल्कि एक भिन्न है।
अत: – 150 इस AP का पद नहीं है
7. उस AP का 31 वाँ पद ज्ञात कीजिए जिसका 11 वाँ पद 38 और 16 वाँ पद 73 है।
समाधान:
मान लीजिये,
11 वाँ पद, a 11 = 38
और 16 वाँ पद, a 16 = 73
हम जानते हैं कि,
ए एन = ए+(एन−1)डी
a 11 = a+(11−1)d
38 = ए+10डी …………………. (मैं)
उसी तरह से,
ए 16 = ए +(16−1) डी
73 = ए +15 डी ………………………………… (ii)
समीकरण (i) को (ii) से घटाने पर , हम प्राप्त करते हैं
35 = 5 डी
डी = 7
समीकरण (i) से हम लिख सकते हैं,
38 = ए +10×(7)
38 - 70 = ए
ए = -32
ए 31 = ए +(31−1) डी
= - 32 + 30 (7)
= - 32 + 210
= 178
अत: 31 वाँ पद 178 है।
8. एक AP में 50 पद हैं जिनमें से तीसरा पद 12 है और अंतिम पद 106 है। 29 वाँ पद ज्ञात कीजिए।
हल: यह देखते हुए कि,
तीसरा पद, a 3 = 12
50 वाँ पद, a 50 = 106
हम जानते हैं कि,
ए एन = ए +( एन -1) डी
ए 3 = ए +(3−1) डी
12 = ए +2 डी ……………………………। (मैं)
उसी तरह से,
a 50 = a +(50−1) d
106 = ए +49 डी । (ii)
समीकरण (i) को (ii) से घटाने पर , हम प्राप्त करते हैं
94 = 47 डी
डी = 2 = सामान्य अंतर
समीकरण (i) से , अब हम लिख सकते हैं,
12 = ए +2(2)
ए = 12−4 = 8
a 29 = a +(29−1) d
ए 29 = 8+(28)2
ए 29 = 8+56 = 64
अत: 29 वाँ पद 64 है।
9. यदि किसी AP के तीसरे और नौवें पद क्रमशः 4 और - 8 हैं। इस AP का कौन सा पद शून्य है।
समाधान:
मान लीजिये,
तीसरा पद, a 3 = 4
और 9 वाँ पद, a 9 = −8
हम जानते हैं कि,
ए एन = ए +( एन -1) डी
इसलिए,
ए 3 = ए +(3−1) डी
4 = ए +2 डी ……………………………………… (i)
ए 9 = ए +(9−1) डी
−8 = ए +8 डी ………………………………………………… (ii)
समीकरण (i) को (ii) से घटाने पर , हम प्राप्त करेंगे,
−12 = 6d
डी = -2
समीकरण (i) से हम लिख सकते हैं,
4 = ए +2(-2)
4 = ए -4
ए = 8
माना इस AP का n वाँ पद शून्य है।
ए एन = ए +( एन -1) डी
0 = 8+( एन -1)(−2)
0 = 8−2 n +2
2 एन = 10
एन = 5
अत: इस AP का 5 वाँ पद 0 है।
10. यदि किसी AP का 17 वाँ पद उसके 10 वें पद से 7 अधिक हो जाता है। सामान्य अंतर ज्ञात कीजिए।
समाधान:
हम जानते हैं कि, एक एपी श्रृंखला के लिए;
ए एन = ए +( एन -1) डी
ए 17 = ए +(17−1) डी
17 पर = + 16d . पर
उसी तरह से,
ए 10 = ए +9 डी
जैसा कि प्रश्न में दिया गया है,
और 17 - और 10 = 7
इसलिए,
( ए +16 डी )-( ए +9 डी ) = 7
7 डी = 7
डी = 1
अतः सार्व अंतर 1 है।
11. AP 3, 15, 27, 39,.. का कौन-सा पद उसके 54 वें पद से 132 अधिक होगा ?
समाधान:
दिया गया AP 3, 15, 27, 39,…
पहला पद, a = 3
सार्व अंतर, d = a 2 - a 1 = 15 - 3 = 12
हम जानते हैं कि,
ए एन = ए +( एन -1) डी
इसलिए,
a 54 = a +(54−1) d
⇒3+(53)(12)
⇒3+636 = 639
एक 54 = 639+132=771
हमें इस AP का पद ज्ञात करना है जो 54 से 132 अधिक है, अर्थात 771।
माना n वाँ पद 771 है।
ए एन = ए +( एन -1) डी
771 = 3+( एन -1)12
768 = ( एन -1)12
( एन -1) = 64
एन = 65
अत: 65 वाँ पद 54 वें पद से 132 अधिक था ।
या कोई अन्य तरीका है;
माना n वाँ पद 54 वें पद से 132 अधिक है ।
एन = 54 + 132/2
= 54 + 11 = 65 वाँ पद
12. दो APs में समान उभयनिष्ठ अंतर हैं। उनके 100 वें पद का अंतर 100 है, उनके 1000 वें पदों में कितना अंतर है?
समाधान:
मान लीजिए, दो APs का पहला पद क्रमशः 1 और 2 है
और इन APs का सामान्य अंतर d है ।
पहले एपी के लिए, हम जानते हैं,
ए एन = ए +( एन -1) डी
इसलिए,
एक 100 = एक 1 +(100−1) डी
= एक 1 + 99डी
एक 1000 = एक 1 +(1000−1) डी
एक 1000 = एक 1 +999 डी
दूसरे एपी के लिए, हम जानते हैं,
ए एन = ए +( एन -1) डी
इसलिए,
एक 100 = एक 2 +(100−1) d
= ए 2 +99 डी
एक 1000 = एक 2 +(1000−1) d
= ए 2 +999 डी
दिया गया है, दो APs के 100 वें पद के बीच का अंतर = 100
इसलिए, ( a 1 +99 d ) - ( a 2 +99 d ) = 100
ए 1 - ए 2 = 100……………………………………………………………….. (i)
दो APs के 1000 वें पदों के बीच अंतर
( ए 1 +999 डी ) - ( ए 2 +999 डी ) = ए 1 - ए 2
समीकरण (i) से ,
यह अंतर, a 1 - a 2 = 100
अत : दोनों AP के 1000 वें पदों के बीच का अंतर 100 होगा।
13. तीन अंकों की कितनी संख्याएँ 7 से विभाज्य हैं?
समाधान:
पहली तीन अंकों की संख्या जो 7 से विभाज्य है, हैं;
पहली संख्या = 105
दूसरी संख्या = 105+7 = 112
तीसरी संख्या = 112+7 =119
इसलिए, 105, 112, 119,…
सभी तीन अंकों की संख्याएँ 7 से विभाज्य हैं और इस प्रकार, ये सभी एक AP के पद हैं जिसका पहला पद 105 और सामान्य अंतर 7 है।
जैसा कि हम जानते हैं, तीन अंकों की सबसे बड़ी संभावित संख्या 999 है।
जब हम 999 को 7 से विभाजित करते हैं, तो शेषफल 5 होगा।
इसलिए, 999-5 = 994 अधिकतम संभव तीन अंकों की संख्या है जो 7 से विभाज्य है।
अब श्रंखला इस प्रकार है।
105, 112, 119,…, 994
माना 994 इस AP का nवाँ पद है
पहला पद, a = 105
सार्व अंतर, d = 7
एक एन = 994
एन =?
जैसा कि हम जानते हैं,
ए एन = ए+(एन−1)डी
994 = 105+(n−1)7
889 = (n−1)7
(एन−1) = 127
एन = 128
अत: 128 तीन अंकों की संख्याएँ 7 से विभाज्य हैं।
14. 10 और 250 के बीच 4 के कितने गुणज हैं?
समाधान:
4 का पहला गुणज जो 10 से बड़ा है, 12 है।
अगला गुणज 16 होगा।
इसलिए, श्रृंखला के रूप में गठित;
12, 16, 20, 24,…
ये सभी 4 से विभाज्य हैं और इस प्रकार, ये सभी एक AP के पद हैं जिसका पहला पद 12 और सार्व अंतर 4 है।
जब हम 250 को 4 से भाग देते हैं, तो शेष 2 प्राप्त होता है। इसलिए, 250 - 2 = 248, 4 से विभाज्य है।
श्रृंखला इस प्रकार है, अब;
12, 16, 20, 24,…, 248
माना 248 इस AP का n वाँ पद है
पहला पद, a = 12
सार्व अंतर, d = 4
एक एन = 248
जैसा कि हम जानते हैं,
ए एन = ए+(एन−1)डी
248 = 12+( एन -1)×4
236/4 = n-1
59 = n-1
एन = 60
इसलिए, 10 और 250 के बीच 4 के 60 गुणज हैं।
15. n के किस मान के लिए, दो APs 63, 65, 67, और 3, 10, 17,… के n वें पद बराबर हैं?
समाधान:
दो एपी के रूप में दिया गया; 63, 65, 67,… और 3, 10, 17,…।
पहला एपी लेना,
63, 65, 67,…
पहला पद, a = 63
सामान्य अंतर, d = a 2 −a 1 = 65−63 = 2
हम जानते हैं, इस AP का n वां पद = a n = a+(n−1)d
ए एन = 63+( एन -1)2 = 63+2 एन -2
ए एन = 61+2 एन ……………………………………। (मैं)
दूसरा एपी लेना,
3, 10, 17,…
पहला पद, a = 3
सामान्य अंतर, d = a 2 - a 1 = 10 - 3 = 7
हम जानते हैं कि,
इस AP का n वाँ पद = 3+( n -1)7
ए एन = 3+7 एन −7
एक एन = 7 एन -4 ………………………………………………… .. (ii)
दिया गया है, इन APs का n वाँ पद एक दूसरे के बराबर है।
इन दोनों समीकरणों की बराबरी करने पर, हम प्राप्त करते हैं,
61+2 n = 7 n −4
61+4 = 5 एन
5 एन = 65
एन = 13
इसलिए, इन दोनों APs के 13 वें पद एक दूसरे के बराबर हैं।
16. उस AP का निर्धारण करें जिसका तीसरा पद 16 है और 7 वाँ पद 5 वें पद से 12 अधिक है।
समाधान:
दिया गया,
तीसरा पद, a 3 = 16
जैसा कि हम जानते हैं,
ए +(3−1) डी = 16
ए +2 डी = 16 ………………………………………। (मैं)
यह दिया गया है कि, 7 वाँ पद 5 वें पद से 12 अधिक है।
ए 7 - ए 5 = 12
[ a +(7−1) d ]−[ a +(5−1) d ]= 12
( ए +6 डी )-( ए +4 डी ) = 12
2डी = 12
डी = 6
समीकरण (i) से, हम प्राप्त करते हैं,
ए +2(6) = 16
ए +12 = 16
ए = 4
इसलिए, AP 4, 10, 16, 22,…
17. AP 3, 8, 13,…, 253 के अंतिम पद से 20 वाँ पद ज्ञात कीजिए।
समाधान:
दिया गया AP है3, 8, 13,…, 253
सामान्य अंतर, डी = 5।
इसलिए, हम दिए गए AP को उल्टे क्रम में इस प्रकार लिख सकते हैं;
253, 248, 243,…, 13, 8, 5
अब नए एपी के लिए,
पहला पद, a = 253
और सार्व अंतर, d = 248 - 253 = -5
एन = 20
इसलिए, nवें पद के सूत्र का उपयोग करते हुए, हम प्राप्त करते हैं,
ए 20 = ए +(20−1) डी
एक 20 = 253+(19)(−5)
एक 20 = 253−95
ए = 158
इसलिए, AP 3, 8, 13,…, 253 के अंतिम पद से 20 वाँ पद । 158 है।
18. एक AP के 4 वें और 8 वें पदों का योग 24 है और 6 वें और 10 वें पदों का योग 44 है। AP के पहले तीन पद ज्ञात कीजिए ।
समाधान:
हम जानते हैं कि, AP का nवाँ पद है;
ए एन = ए +( एन -1) डी
ए 4 = ए + (4−1) डी
ए 4 = ए +3 डी
इसी तरह हम लिख सकते हैं,
ए 8 = ए +7 डी
ए 6 = ए +5 डी
ए 10 = ए +9 डी
मान लीजिये,
ए 4 + ए 8 = 24
ए+3डी+ए+7डी = 24
2a+10d = 24
a+5d = 12 (i)
ए 6 + ए 10 = 44
ए +5डी+ए+9डी = 44
2a+14d = 44
ए + 7 डी = 22 …………………………………… .. (ii)
समीकरण (i) को (ii) से घटाने पर , हम प्राप्त करते हैं,
2d = 22 - 12
2डी = 10
डी = 5
समीकरण (i) से , हम प्राप्त करते हैं,
ए +5 डी = 12
ए +5(5) = 12
ए +25 = 12
ए = -13
a 2 = a + d = − 13+5 = −8
ए 3 = ए 2 + डी = -8+5 = -3
इसलिए, इस AP के पहले तीन पद −13, −8 और −3 हैं।
19. सुब्बा राव ने 1995 में 5000 रुपये के वार्षिक वेतन पर काम शुरू किया और प्रत्येक वर्ष 200 रुपये की वृद्धि प्राप्त की। किस वर्ष उसकी आय 7000 रुपये तक पहुँच गई?
समाधान:
दिए गए प्रश्न से यह देखा जा सकता है कि सुब्बा राव की आय में हर साल 200 रुपये की वृद्धि होती है और इसलिए, एक एपी बनता है।
इसलिए, 1995 के बाद, प्रत्येक वर्ष के वेतन हैं;
5000, 5200, 5400,…
यहाँ, पहला पद, a = 5000
और सार्व अंतर, d = 200
माना n वें वर्ष के बाद , उसका वेतन 7000 रुपये है।
अत: AP के n वें पद के सूत्र से,
ए एन = ए +( एन -1) डी
7000 = 5000+( एन -1)200
200( एन -1)= 2000
( एन -1) = 10
एन = 11
अतः 11वें वर्ष में उनका वेतन 7000 रुपये होगा।
20. रामकली ने एक वर्ष के पहले सप्ताह में 5 रुपये की बचत की और फिर अपनी साप्ताहिक बचत में 1.75 रुपये की वृद्धि की। यदि n वें सप्ताह में, उसकी साप्ताहिक बचत 20.75 रुपये हो जाती है, तो n ज्ञात कीजिए।
समाधान:
यह देखते हुए, रामकाली ने पहले सप्ताह में 5 रुपये की बचत की और फिर प्रत्येक सप्ताह 1.75 रुपये की बचत करना शुरू कर दिया।
अत,
पहला पद, a = 5
और सार्व अंतर, d = 1.75
भी दिया,
एक एन = 20.75
खोजें, n = ?
जैसा कि हम जानते हैं, n वें पद के सूत्र से,
ए एन = ए +( एन -1) डी
इसलिए,
20.75 = 5+( एन -1)×1.75
15.75 = ( एन -1)×1.75
( एन -1) = 15.75/1.75 = 1575/175
= 63/7 = 9
एन -1 = 9
एन = 10
अत: n 10 है।
Exercise - 5.3 पृष्ठ: 112
1. निम्नलिखित APs का योग ज्ञात कीजिए।
(i) 2, 7, 12,…., से 10 पद।
(ii) - 37, − 33, − 29 ,…, 12 पदों तक
(iii) 0.6, 1.7, 2.8 ,…….., 100 पदों तक
(iv) 1/15, 1/12, 1/10,… … , 11 पदों तक
समाधान:
(i) दिया गया है, 2, 7, 12 ,…, से 10 पदों तक
इसके लिए एपी,
पहला पद, a = 2
और सार्व अंतर, d = a 2 - a 1 = 7−2 = 5
एन = 10
हम जानते हैं कि AP श्रृंखला में nवें पद के योग का सूत्र है,
एस एन = एन/2 [2ए +(एन-1)डी]
एस 10 = 10/2 [2(2)+(10 -1)×5]
= 5[4+(9)×(5)]
= 5 × 49 = 245
(ii) दिया गया है, −37, −33, −29 ,…, से 12 पदों तक
इसके लिए एपी,
पहला पद, a = -37
और सार्व अंतर, d = a 2 - a 1
डी = (-33)-(-37)
= - 33 + 37 = 4
एन = 12
हम जानते हैं कि AP श्रृंखला में nवें पद के योग का सूत्र है,
एस एन = एन/2 [2ए+(एन-1)डी]
एस 12 = 12/2 [2 (-37) + (12-1) × 4]
= 6[-74+11×4]
= 6[-74+44]
= 6(-30) = -180
(iii) दिया गया है, 0.6, 1.7, 2.8,…, से 100 पदों तक
इसके लिए एपी,
पहला पद, a = 0.6
सामान्य अंतर, d = a 2 - a 1 = 1.7 - 0.6 = 1.1
एन = 100
हम जानते हैं कि AP श्रृंखला में nवें पद के योग का सूत्र है,
एस एन = एन/2[2ए +(एन-1)डी]
एस 12 = 50/2 [1.2+ (99) × 1.1]
= 50 [1.2+108.9]
= 50 [110.1]
= 5505
(iv) दिया गया है, 1/15, 1/12, 1/10, …… , से 11 पदों तक
इसके लिए एपी,
पहला पद, a = 1/5
सामान्य अंतर, d = a 2 –a 1 = (1/12)-(1/5) = 1/60
और पदों की संख्या n = 11
हम जानते हैं कि AP श्रृंखला में nवें पद के योग का सूत्र है,
एस एन = एन / 2 [2ए + ( एन -1) डी ]
= 11/2(2/15 + 10/60)
= 11/2 (9/30)
= 33/20
2. नीचे दी गई राशि ज्ञात कीजिए :
(ii) 34 + 32 + 30 + .. + 10
(iii) - 5 + (- 8) + (- 11) + ………… + (- 230)
समाधान:
(मैं)
पहला पद, a = 7
n वाँ पद, a n = 84
मान लीजिए इस AP का n वाँ पद 84 है , तो n वें पद के सूत्र के अनुसार,
ए एन = ए (एन -1) डी
84 = 7+(एन – 1)×7/2
77 = (एन-1)×7/2
22 = n−1
एन = 23
हम जानते हैं कि, n पदों का योग है;
एस एन = एन/2 (ए + एल), एल = 84
एस एन = 23/2 (7+84)
एस एन = (23×91/2) = 2093/2
(ii) दिया गया है, 34 + 32 + 30 + ……….. + 10
इसके लिए एपी,
पहला पद, a = 34
सार्व अंतर, d = a 2 −a 1 = 32−34 = −2
n वाँ पद, a n = 10
मान लीजिए 10 इस AP का n वाँ पद है, इसलिए,
ए एन = ए +(एन−1)डी
10 = 34+(n−1)(−2)
−24 = (एन -1)(−2)
12 = एन -1
एन = 13
हम जानते हैं कि, n पदों का योग है;
एस एन = एन/2 (ए +एल), एल = 10
= 13/2 (34 + 10)
= (13×44/2) = 13 × 22
= 286
(iii) दिया गया है, (−5) + (−8) + (−11) + …………… + (−230)
इसके लिए एपी,
पहला पद, a = −5
nवाँ पद, a n = −230
सामान्य अंतर, d = a 2 −a 1 = (−8)−(−5)
d = − 8+5 = −3
माना −230 इस AP का n वाँ पद है, और n वें पद के सूत्र से हम जानते हैं,
ए एन = ए +( एन -1) डी
−230 = − 5+( n −1)(−3)
−225 = ( n −1)(−3)
( एन -1) = 75
एन = 76
और, n पद का योग,
एस एन = एन / 2 ( ए + एल )
= 76/2 [(-5) + (-230)]
= 38(-235)
= -8930
3. एक AP में
(i) a = 5, d = 3, a n = 50 दिया गया है, n और S n ज्ञात कीजिए ।
(ii) दिया गया a = 7, a 13 = 35, d और S 13 ज्ञात कीजिए ।
(iii) दिया गया a 12 = 37, d = 3, a और S 12 खोजें ।
(iv) दिया गया है a 3 = 15, S 10 = 125, d और a 10 खोजें ।
(v) दिया गया d = 5, S 9 = 75, a और a 9 ज्ञात कीजिए ।
(vi) दिया गया a = 2, d = 8, S n = 90, n और a n ज्ञात कीजिए ।
(vii) दिया गया a = 8, a n = 62, S n = 210, n और d ज्ञात कीजिए ।
(viii) दिया गया है a n = 4, d = 2, S n = - 14, n और a ज्ञात कीजिए ।
(ix) दिया गया a = 3, n = 8, S = 192, d ज्ञात कीजिए ।
(x) दिया गया है l = 28, S = 144 और कुल 9 पद हैं। ए खोजें ।
समाधान:
(i) दिया गया है कि, a = 5, d = 3, a n = 50
जैसा कि हम जानते हैं, किसी AP में nवें पद के सूत्र से,
ए एन = ए +( एन -1) डी ,
इसलिए, दिए गए मानों को रखने पर, हम प्राप्त करते हैं,
50 = 5+( एन -1)×3
3 ( एन -1) = 45
एन -1 = 15
एन = 16
अब, n पदों का योग,
एस एन = एन / 2 ( ए + ए एन )
एस एन = 16/2 (5 + 50) = 440
(ii) दिया गया है कि, a = 7, a 13 = 35
जैसा कि हम जानते हैं, किसी AP में nवें पद के सूत्र से,
ए एन = ए +( एन -1) डी ,
इसलिए, दिए गए मानों को रखने पर, हम प्राप्त करते हैं,
⇒ 35 = 7+(13-1) डी
12 डी = 28
डी = 28/12 = 2.33
अब, S n = n /2 ( a + a n )
एस 13 = 13/2 (7+35) = 273
(iii) दिया गया है कि, a 12 = 37, d = 3
जैसा कि हम जानते हैं, किसी AP में n वें पद के सूत्र से,
ए एन = ए +( एन -1) डी ,
इसलिए, दिए गए मानों को रखने पर, हम प्राप्त करते हैं,
⇒ ए 12 = ए +(12−1)3
37 = ए +33
ए = 4
अब, nवें पद का योग,
एस एन = एन / 2 ( ए + ए एन )
एस एन = 12/2 (4+37)
= 246
(iv) दिया गया है कि, a 3 = 15, एस 10 = 125
जैसा कि हम जानते हैं, किसी AP में nवें पद के सूत्र से,
ए एन = ए +( एन -1) डी ,
इसलिए, दिए गए मानों को रखने पर, हम प्राप्त करते हैं,
ए 3 = ए +(3−1) डी
15 = ए +2 डी ………………………….. (i)
nवें पद का योग,
एस एन = एन / 2 [2 ए +( एन -1) डी ]
एस 10 = 10/2 [2 ए +(10-1) डी ]
125 = 5(2 ए +9 डी )
25 = 2 ए + 9 डी ……………………….. (ii)
समीकरण (i) को (ii) से गुणा करने पर , हम प्राप्त करेंगे;
30 = 2 ए +4 डी ………………………। (iii)
समीकरण (iii) को (ii) से घटाने पर , हम प्राप्त करते हैं,
-5 = 5 डी
डी = -1
समीकरण (i) से ,
15 = ए +2(−1)
15 = एक -2
a = 17 = पहला पद
ए 10 = ए +(10−1) डी
एक 10 = 17+ (9) (- 1)
और 10 = 17−9 = 8
(v) दिया गया है कि, d = 5, S 9 = 75
जैसे, AP में n पदों का योग है,
एस एन = एन / 2 [2 ए +( एन -1) डी ]
इसलिए, पहले नौ पदों का योग है;
एस 9 = 9/2 [2 ए + (9-1) 5 ]
25 = 3 ( ए +20)
25 = 3a +60
3ए = 25−60
ए = -35/3
जैसा कि हम जानते हैं, n वें पद को इस प्रकार लिखा जा सकता है;
ए एन = ए +( एन -1) डी
ए 9 = ए + (9−1) (5)
= -35/3+8(5)
= -35/3+40
= (35+120/3) = 85/3
(vi) दिया गया है कि, a = 2, d = 8, S n = 90
जैसे, एक AP में n पदों का योग है,
एस एन = एन / 2 [2 ए +( एन -1) डी ]
90 = एन / 2 [2 ए +( एन -1) डी ]
⇒ 180 = n (4+8 n -8) = n (8 n -4) = 8 n 2 -4 n
⇒ 8 एन 2 -4 एन - 180 = 0
2 एन 2 - एन -45 = 0
⇒ 2 एन 2 -10 एन +9 एन -45 = 0
2 एन ( एन -5) + 9 ( एन -5) = 0
( एन -5)(2 एन +9) = 0
अतः, n = 5 (क्योंकि n केवल एक धनात्मक पूर्णांक है)
∴ ए 5 = 8+5×4 = 34
(vii) दिया गया है कि, a = 8, a n = 62, S n = 210
जैसे, एक AP में n पदों का योग है,
एस एन = एन / 2 ( ए + ए एन )
210 = एन / 2 (8 +62)
⇒ 35 एन = 210
एन = 210/35 = 6
अब, 62 = 8+5 d
⇒ 5 डी = 62-8 = 54
डी = 54/5 = 10.8
(viii) दिया गया है कि, n वां पद, a n = 4, उभयनिष्ठ अंतर, d = 2, n पदों का योग, S n = −14।
जैसा कि हम जानते हैं, किसी AP में n वें पद के सूत्र से,
ए एन = ए +( एन -1) डी ,
इसलिए, दिए गए मानों को रखने पर, हम प्राप्त करते हैं,
4 = ए +( एन -1)2
4 = ए +2 एन -2
ए +2 एन = 6
ए = 6 - 2 एन …………………………………। (मैं)
जैसा कि हम जानते हैं, n पदों का योग है;
एस एन = एन / 2 ( ए + ए एन )
-14 = एन / 2 ( ए + 4 )
-28 = एन ( ए +4)
−28 = n (6 −2 n +4) {समीकरण (i) से }
-28 = एन (-2 एन +10)
−28 = -2 n 2 +10 n
2 एन 2 -10 एन - 28 = 0
n 2 −5 n −14 = 0
n 2 −7 n+ 2 n −14 = 0
n ( n −7)+2( n −7) = 0
( एन −7)( एन +2) = 0
या तो n - 7 = 0 या n + 2 = 0
एन = 7 या एन = -2
हालाँकि, n न तो ऋणात्मक हो सकता है और न ही भिन्नात्मक।
इसलिए, n = 7
समीकरण (i) से , हम प्राप्त करते हैं
ए = 6−2 एन
ए = 6−2(7)
= 6−14
= −8
(ix) दिया गया है कि, पहला पद, a = 3,
पदों की संख्या, n = 8
और n पदों का योग, S = 192
जैसा कि हम जानते हैं,
एस एन = एन / 2 [2 ए +( एन -1) डी ]
192 = 8/2 [2×3+(8 -1) घ ]
192 = 4 [6 +7 घ ]
48 = 6+7 डी
42 = 7 डी
डी = 6
(x) दिया गया है कि, l = 28, S = 144 और कुल 9 पद हैं।
n पदों का योग सूत्र,
एस एन = एन / 2 ( ए + एल )
144 = 9/2( ए +28)
(16) ×(2) = ए +28
32 = ए +28
ए = 4
4. AP के कितने पद हैं। 9, 17, 25 … को 636 का योग देने के लिए लिया जाना चाहिए?
समाधान:
माना AP के n पद हैं। 9, 17, 25…
इसके लिए एपी,
पहला पद, a = 9
सामान्य अंतर, d = a 2 - a 1 = 17−9 = 8
जैसे, n पदों का योग है;
एस एन = एन / 2 [2 ए +( एन -1) डी ]
636 = n /2 [2× a +(8-1)×8]
636 = एन /2 [18+( एन -1)×8]
636 = n [9 +4 n −4]
636 = एन (4 एन +5)
4 एन 2 +5 एन -636 = 0
4 एन 2 +53 एन −48 एन −636 = 0
एन (4 एन + 53) -12 (4 एन + 53) = 0
(4 एन +53) ( एन -12) = 0
या तो 4 n +53 = 0 या n -12 = 0
एन = (-53/4) या एन = 12
n ऋणात्मक या भिन्न नहीं हो सकता है, इसलिए केवल n = 12 है।
5. किसी AP का प्रथम पद 5 है, अंतिम पद 45 है और योग 400 है। पदों की संख्या और सार्व अंतर ज्ञात कीजिए।
समाधान:
मान लीजिये,
पहला पद, a = 5
अंतिम पद, एल = 45
एपी का योग, एस एन = 400
जैसा कि हम जानते हैं, AP सूत्र का योग होता है;
एस एन = एन / 2 ( ए + एल )
400 = एन /2(5+45)
400 = एन / 2(50)
पदों की संख्या, n =16
जैसा कि हम जानते हैं, AP श्रंखला का अंतिम पद इस प्रकार लिखा जा सकता है;
एल = ए+ ( एन -1) डी
45 = 5 +(16 -1) डी
40 = 15 डी
सामान्य अंतर, डी = 40/15 = 8/3
6. एक AP का पहला और अंतिम पद क्रमशः 17 और 350 है। यदि सार्व अंतर 9 है, तो कितने पद हैं और उनका योग क्या है?
समाधान:
मान लीजिये,
पहला पद, a = 17
अंतिम पद, एल = 350
सामान्य अंतर, d = 9
मान लीजिए AP में n पद हैं, इस प्रकार अंतिम पद का सूत्र इस प्रकार लिखा जा सकता है;
एल = ए+ ( एन -1) डी
350 = 17+( एन -1)9
333 = ( एन −1)9
( एन -1) = 37
एन = 38
एस एन = एन / 2 ( ए + एल )
एस 38 = 38/2 (17+350)
= 19×367
= 6973
इस प्रकार, इस AP में 38 पद हैं और इस AP के पदों का योग 6973 है।
7. एक AP के पहले 22 पदों का योग ज्ञात कीजिए जिसमें d = 7 और 22 वाँ पद 149 है।
हल:
दिया गया है, सार्व अंतर, d = 7
22 वाँ पद, a 22 = 149
पहले 22 पदों का योग, S 22 = ?
nवें पद के सूत्र से,
ए एन = ए +( एन -1) डी
ए 22 = ए + (22−1) डी
149 = ए +21×7
149 = ए +147
ए = 2 = पहला पद
n पदों का योग,
एस एन = एन / 2 ( ए + ए एन )
एस 22 = 22/2 (2+149)
= 11×151
= 1661
8. एक AP के पहले 51 पदों का योग ज्ञात कीजिए जिसका दूसरा और तीसरा पद क्रमशः 14 और 18 है।
समाधान:
मान लीजिये,
दूसरा पद, a 2 = 14
तीसरा पद, a 3 = 18
सामान्य अंतर, d = a 3 - a 2 = 18−14 = 4
ए 2 = ए + डी
14 = ए +4
ए = 10 = पहला पद
एन शर्तों का योग;
एस एन = एन / 2 [2 ए + ( एन -1) डी ]
एस 51 = 51/2 [2 × 10 (51-1) 4]
= 51/2 [20+(50)×4]
= 51 × 220/2
= 51 × 110
= 5610
9. यदि किसी AP के प्रथम 7 पदों का योग 49 है और 17 पदों का योग 289 है, तो प्रथम n पदों का योग ज्ञात कीजिए।
समाधान:
मान लीजिये,
एस 7 = 49
एस 17 = 289
हम जानते हैं, n पदों का योग;
एस एन = एन / 2 [2 ए + ( एन -1) डी ]
इसलिए,
एस 7 = 7/2 [2 ए + ( एन -1) डी ]
एस 7 = 7/2 [2 ए + (7 -1) डी ]
49 = 7/2 [2 ए +6 डी ]
7 = ( ए +3 डी )
ए + 3 डी = 7 …………………………………। (मैं)
उसी तरह से,
एस 17 = 17/2 [2 ए + (17-1) डी ]
289 = 17/2 (2 ए +16 डी )
17 = ( ए +8 डी )
ए +8 डी = 17 ………………………। (ii)
समीकरण (i) को समीकरण (ii) से घटाना ,
5 डी = 10
डी = 2
समीकरण (i) से , हम इसे इस प्रकार लिख सकते हैं;
ए +3(2) = 7
ए+ 6 = 7
ए = 1
अत,
एस एन = एन / 2 [2 ए + ( एन -1) डी ]
= n /2[2(1)+( n – 1)×2]
= n /2(2+2 n -2)
= एन /2(2 एन )
= एन 2
10. दिखाएँ कि a 1 , a 2 …, a n , … एक AP बनाते हैं जहाँ n को नीचे परिभाषित किया गया है
(i) a n = 3+4 n
(ii) a n = 9−5 n
प्रत्येक स्थिति में प्रथम 15 पदों का योग भी ज्ञात कीजिए।
समाधान:
(i) ए एन = 3+4 एन
ए 1 = 3 + 4 (1) = 7
ए 2 = 3+4(2) = 3+8 = 11
और 3 = 3 + 4 (3) = 3 + 12 = 15
ए 4 = 3+4(4) = 3+16 = 19
हम यहां देख सकते हैं, शर्तों के बीच सामान्य अंतर हैं;
ए 2 - ए 1 = 11−7 = 4
ए 3 - ए 2 = 15−11 = 4
a 4 - a 3 = 19−15 = 4
इसलिए, a k + 1 - a k हर बार एक ही मान होता है। इसलिए, यह एक AP है जिसका सार्व अंतर 4 है और पहला पद 7 है।
अब, हम जानते हैं, nवें पद का योग है;
एस एन = एन / 2 [2 ए + ( एन -1) डी ]
एस 15 = 15/2 [2 (7)+(15-1) × 4]
= 15/2[(14)+56]
= 15/2(70)
= 15×35
= 525
(ii) एक n = 9−5 n
a 1 = 9−5 × 1 = 9−5 = 4
a 2 = 9−5×2 = 9−10 = -1
एक 3 = 9−5 × 3 = 9−15 = −6
a4 = 9−5× 4 = 9−20 = -11
हम यहां देख सकते हैं, शर्तों के बीच सामान्य अंतर हैं;
ए 2 - ए 1 = -1−4 = -5
a 3 - a 2 = −6−(−1) = −5
a 4 - a 3 = −11−(−6) = −5
इसलिए, a k + 1 - a k हर बार समान होता है। इसलिए, यह एक AP है जिसका सार्व अंतर −5 है और पहला पद 4 है।
अब, हम जानते हैं, nवें पद का योग है;
एस एन = एन / 2 [2 ए +( एन -1) डी ]
एस 15 = 15/2 [2 (4) +(15 -1) (-5)]
= 15/2[8 +14(-5)]
= 15/2(8-70)
= 15/2(-62)
= 15(-31)
= -465
11. यदि किसी AP के पहले n पदों का योग 4 n - n 2 है, तो पहला पद क्या है (अर्थात S 1 )? पहले दो पदों का योग क्या है? दूसरा कार्यकाल क्या है? इसी तरह तीसरे , दसवें और n वें पदों को खोजें ।
समाधान:
मान लीजिये,
एस एन = 4 एन - एन 2
पहला पद, a = S 1 = 4(1) - (1) 2 = 4−1 = 3
पहले दो पदों का योग = S 2 = 4(2)-(2) 2 = 8−4 = 4
दूसरा पद, a 2 = S 2 - S 1 = 4−3 = 1
सामान्य अंतर, d = a 2 - a = 1−3 = -2
एन वाँ पद, a n = a +( n −1) d
= 3+( एन -1)(−2)
= 3−2 n +2
= 5−2 एन
इसलिए, एक 3 = 5−2(3) = 5-6 = -1
और 10 = 5−2 (10) = 5−20 = −15
अत: प्रथम दो पदों का योग 4 है। दूसरा पद 1 है।
तीसरा , 10 वां , और n वां पद क्रमशः −1, −15, और 5 − 2 n हैं।
12. 6 से विभाज्य पहले 40 धनात्मक पूर्णांकों का योग ज्ञात कीजिए।
समाधान:
वे धनात्मक पूर्णांक जो 6 से विभाज्य हैं, 6, 12, 18, 24….
हम यहाँ देख सकते हैं कि यह श्रृंखला एक AP बनाती है जिसका पहला पद 6 है और सार्व अंतर 6 है।
ए = 6
डी = 6
एस 40 = ?
n पदों के योग के सूत्र से, हम जानते हैं,
एस एन = एन / 2 [2 ए + ( एन -1) डी ]
इसलिए, n = 40 रखने पर, हम प्राप्त करते हैं,
एस 40 = 40/2 [2(6)+(40-1)6]
= 20[12+(39)(6)]
= 20(12+234)
= 20×246
= 4920
13. 8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
समाधान:
8 के गुणज 8, 16, 24, 32…
श्रृंखला AP के रूप में है, जिसका पहला पद 8 और सार्व अंतर 8 है।
इसलिए, ए = 8
डी = 8
एस 15 =?
nवें पद के योग के सूत्र से हम जानते हैं,
एस एन = एन / 2 [2 ए +( एन -1) डी ]
एस 15 = 15/2 [2 (8) + (15-1) 8]
= 15/2[16 +(14)(8)]
= 15/2[16 +112]
= 15(128)/2
= 15 × 64
= 960
14. 0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
समाधान:
0 और 50 के बीच की विषम संख्याएँ 1, 3, 5, 7, 9…49 हैं।
इसलिए, हम देख सकते हैं कि ये विषम संख्याएँ AP . के रूप में हैं
अत,
पहला पद, a = 1
सामान्य अंतर, डी = 2
अंतिम पद, l = 49
अंतिम पद के सूत्र से, हम जानते हैं,
एल = ए +( एन -1) डी
49 = 1+( एन -1)2
48 = 2( एन -1)
एन -1 = 24
n = 25 = पदों की संख्या
nवें पद के योग के सूत्र से हम जानते हैं,
एस एन = एन / 2 ( ए + एल )
एस 25 = 25/2 (1+49)
= 25(50)/2
=(25)(25)
= 625
15. निर्माण कार्य पर एक अनुबंध एक निश्चित तिथि से आगे पूरा होने में देरी के लिए दंड को निम्नानुसार निर्दिष्ट करता है: रु। पहले दिन के लिए 200 रु. दूसरे दिन 250 रु. तीसरे दिन के लिए 300, आदि, प्रत्येक सफल दिन के लिए जुर्माना रु। पिछले दिन की तुलना में 50 अधिक। यदि ठेकेदार ने काम में 30 दिन की देरी की है तो उसे कितनी राशि पेनल्टी के रूप में देनी होगी।
समाधान:
हम देख सकते हैं, कि दिए गए दंड AP के रूप में हैं जिनका पहला पद 200 है और सामान्य अंतर 50 है।
इसलिए, ए = 200 और डी = 50
यदि ठेकेदार ने काम में 30 दिन की देरी की है तो जुर्माना देना होगा = एस 30
nवें पद के योग के सूत्र से हम जानते हैं,
एस एन = एन / 2 [2 ए + ( एन -1) डी ]
इसलिए,
एस 30 = 30/2[2(200)+(30 - 1)50]
= 15[400+1450]
= 15(1850)
= 27750
इसलिए ठेकेदार को 27750 रुपए अर्थदंड के रूप में देने होंगे।
16. एक स्कूल के छात्रों को उनके समग्र शैक्षणिक प्रदर्शन के लिए सात नकद पुरस्कार देने के लिए 700 रुपये की राशि का उपयोग किया जाना है। यदि प्रत्येक पुरस्कार अपने पूर्ववर्ती पुरस्कार से 20 रुपये कम है, तो प्रत्येक पुरस्कार का मूल्य ज्ञात कीजिए।
समाधान:
माना प्रथम पुरस्कार की कीमत रु. पी .
दूसरे पुरस्कार की लागत = रु. पी - 20
और तीसरे पुरस्कार की लागत = रु. पी -40
हम देख सकते हैं कि इन पुरस्कारों की लागत AP के रूप में है, जिसमें −20 का सामान्य अंतर है और पहला पद P है।
इस प्रकार, ए = पी और डी = -20
दिया गया है, S 7 = 700
nवें पद के योग के सूत्र से हम जानते हैं,
एस एन = एन / 2 [2 ए + ( एन -1) डी ]
7/2 [2 ए + (7 - 1) डी ] = 700
ए + 3(−20) = 100
ए -60 = 100
ए = 160
इसलिए, प्रत्येक पुरस्कार का मूल्य 160 रुपये, 140 रुपये, 120 रुपये, 100 रुपये, 80 रुपये, 60 रुपये और 40 रुपये था।
17. एक स्कूल में छात्रों ने वायु प्रदूषण को कम करने के लिए स्कूल के अंदर और आसपास पेड़ लगाने के बारे में सोचा। यह निर्णय लिया गया कि जितने वृक्ष प्रत्येक वर्ग के प्रत्येक वर्ग द्वारा लगाए जाएंगे, उतने ही उस वर्ग के होंगे, जिसमें वे अध्ययन कर रहे हैं, उदाहरण के लिए, कक्षा I का एक वर्ग 1 पेड़ लगाएगा, कक्षा II का एक वर्ग लगाएगा। बारहवीं कक्षा तक 2 पेड़ लगाएं और इसी तरह। प्रत्येक वर्ग के तीन खंड हैं। विद्यार्थी कितने पौधे लगाएंगे?
समाधान:
यह देखा जा सकता है कि छात्रों द्वारा लगाए गए पेड़ों की संख्या एक एपी में है।
1, 2, 3, 4, 5 ………………..12
पहला पद, a = 1
सामान्य अंतर, d = 2−1 = 1
एस एन = एन / 2 [2 ए +( एन -1) डी ]
एस 12 = 12/2 [2 (1) + (12-1) (1)]
= 6(2+11)
= 6(13)
= 78
इसलिए, वर्गों के 1 खंड द्वारा लगाए गए पेड़ों की संख्या = 78
वर्गों के 3 वर्गों द्वारा लगाए गए पेड़ों की संख्या = 3×78 = 234
इसलिए विद्यार्थियों द्वारा 234 पेड़ लगाए जाएंगे।
18. एक सर्पिल क्रमिक अर्धवृत्तों से बना होता है, जिसके केंद्र बारी-बारी से A और B पर होते हैं, केंद्र A से त्रिज्या 0.5, 1.0 सेमी, 1.5 सेमी, 2.0 सेमी, ……… के साथ शुरू होता है जैसा कि चित्र में दिखाया गया है। तेरह क्रमागत अर्धवृत्तों से बने ऐसे सर्पिल की कुल लंबाई कितनी है? ( = 22/7) लें
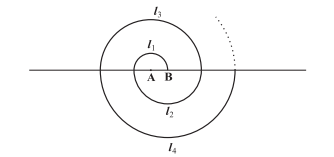
समाधान:
हम जानते है,
अर्धवृत्त का परिमाप = r
इसलिए,
पी 1 = (0.5) = / 2 सेमी
पी 2 = (1) = सेमी
पी 3 = (1.5) = 3π / 2 सेमी
जहां, P 1, P 2 , P 3 अर्धवृत्तों की लंबाई हैं।
इसलिए हमें यहां एक श्रृंखला मिली, जैसे,
/2, , 3π / 2, 2π,…।
पी 1 = / 2 सेमी
पी 2 = π सेमी
सामान्य अंतर, डी = पी 2 - पी 1 = - π / 2 = / 2
पहला पद = पी 1 = ए = π/2 सेमी
एन टर्म फॉर्मूला के योग से, हम जानते हैं,
एस एन = एन / 2 [2 ए + ( एन -1) डी ]
अत: 13 क्रमागत वृत्तों की लंबाई का योग है;
एस 13 = 13/2 [2 (π / 2) + (13 - 1) / 2]
= 13/2 [π + 6π ]
= 13/2 (7π)
= 13/2 × 7 × 22/7
= 143 सेमी
19. 200 लट्ठों को इस प्रकार रखा गया है: 20 लट्ठे नीचे की पंक्ति में, 19 अगली पंक्ति में, 18 लट्ठे उसके आगे की पंक्ति में आदि। 200 लट्ठों को कितनी पंक्तियों में रखा गया है और शीर्ष पंक्ति में कितने लट्ठे हैं?
समाधान:
हम देख सकते हैं कि पंक्तियों में लॉग की संख्या AP20, 19, 18…
दिए गए एपी के लिए,
पहला पद, a = 20 और सार्व अंतर, d = a 2 - a 1 = 19−20 = -1
मान लें कि कुल 200 लॉग्स को n पंक्तियों में रखा गया है।
इस प्रकार, एस एन = 200
nवें पद के सूत्र के योग से,
एस एन = एन / 2 [2 ए +( एन -1) डी ]
एस 12 = 12/2 [2(20)+( एन -1)(-1)]
400 = n (40− n +1)
400 = एन (41- एन )
400 = 41 एन - एन 2
एन 2 −41 एन + 400 = 0
एन 2 −16 एन -25 एन +400 = 0
n ( n −16)−25( n −16) = 0
( एन −16) ( एन −25) = 0
या तो ( n −16) = 0 या n −25 = 0
एन = 16 या एन = 25
nवें पद के सूत्र से,
ए एन = ए +( एन -1) डी
ए 16 = 20+ (16−1) (- 1)
एक 16 = 20−15
एक 16 = 5
इसी प्रकार, 25 वें पद को इस प्रकार लिखा जा सकता है;
एक 25 = 20+(25−1)(−1)
एक 25 = 20−24
= - 4
यह देखा जा सकता है, 16 वीं पंक्ति में लट्ठों की संख्या 5 है क्योंकि संख्याएँ ऋणात्मक नहीं हो सकती हैं।
अतः 200 लट्ठों को 16 पंक्तियों में रखा जा सकता है और 16 वीं पंक्ति में लट्ठों की संख्या 5 है।
20. एक आलू दौड़ में, एक बाल्टी प्रारंभिक बिंदु पर रखी जाती है, जो पहले आलू से 5 मीटर की दूरी पर होती है और अन्य आलू एक सीधी रेखा में 3 मीटर की दूरी पर रखे जाते हैं। लाइन में दस आलू हैं।
एक प्रतियोगी बाल्टी से शुरू करता है, निकटतम आलू को उठाता है, उसके साथ वापस दौड़ता है, उसे बाल्टी में गिराता है, अगले आलू को लेने के लिए वापस दौड़ता है, बाल्टी में उसे गिराने के लिए दौड़ता है, और वह उसी तरह से तब तक जारी रहता है जब तक सारे आलू बाल्टी में हैं। प्रतियोगी को कुल कितनी दूरी तय करनी है?
[संकेत: पहला आलू और दूसरा आलू लेने के लिए, एक प्रतियोगी द्वारा चलाई गई कुल दूरी (मीटर में) 2×5+2×(5+3) है]
समाधान:
बाल्टी से आलू की दूरी 5, 8, 11, 14… है, जो AP के रूप में है।
दिया गया है, इन आलूओं को इकट्ठा करने के लिए प्रतियोगी द्वारा चलाई गई दूरी उस दूरी की दुगुनी है जिस पर आलू रखे गए हैं।
इसलिए, चलाई जाने वाली दूरी, आलू की दूरी के बराबर, को इस प्रकार लिखा जा सकता है;
10, 16, 22, 28, 34, ……….
इसलिए, पहला पद, a = 10 और d = 16−10 = 6
एस10 = ?
n पदों के योग के सूत्र से, हम जानते हैं,
एस 10 \u003d 10/2 [2 (10) + (10 -1) (6)]
= 5[20+54]
= 5(74)
= 370
इसलिए प्रतियोगी कुल 370 मीटर की दूरी तय करेगा।
Exercise - 5.4 पृष्ठ: 115
1. एपी का कौन सा पद: 121, 117, 113, . . ., इसका पहला ऋणात्मक पद है? [संकेत: n < 0 के लिए n खोजें]
समाधान:
दिया गया AP श्रंखला 121, 117, 113, . . ।,
अत: प्रथम पद a = 121
सामान्य अंतर, d = 117-121= -4
nवें पद के सूत्र से,
ए एन = ए +( एन -1) डी
इसलिए,
एक n = 121+(n−1)(-4)
= 121-4एन + 4
= 125-4n
श्रृंखला का पहला ऋणात्मक पद ज्ञात करने के लिए, a n <0
इसलिए,
125-4n <0
125 < 4n
एन>125/4
एन>31.25
इसलिए, श्रृंखला का पहला ऋणात्मक पद 32 वां पद है।
2. एक AP के तीसरे और सातवें पदों का योग 6 है और उनका गुणनफल 8 है। AP के पहले सोलह पदों का योग ज्ञात कीजिए।
समाधान:
दिए गए कथनों से हम लिख सकते हैं,
ए 3 + ए 7 = 6 …………………………….(i)
और
ए 3 × ए 7 = 8 ………………………….. (ii)
nवें पद के सूत्र से,
ए एन = ए +( एन -1) डी
तीसरा पद, a 3 = a+(3 -1)d
ए 3 = ए + 2 डी ……………………… (iii)
और सातवाँ पद, a7= a+(7-1)d
ए 7 = ए + 6 डी ……………………… .. (iv)
समीकरण (iii) और (iv) से, समीकरण (i) रखने पर, हम प्राप्त करते हैं,
ए+2डी +ए+6डी = 6
2a+8d = 6
ए+4डी=3
या
ए = 3-4डी ………………………………… (वी)
फिर से eq.(iii) और (iv) को eq में रखकर। (ii), हम प्राप्त करते हैं,
(ए+2डी)×(ए+6डी) = 8
समीकरण (v) से a का मान रखने पर, हम प्राप्त करते हैं,
(3–4d +2d)×(3–4d+6d) = 8
(3 -2d)×(3+2d) = 8
3 2 - 2d 2 = 8
9 - 4डी 2 = 8
4d 2 = 1
डी = 1/2 या -1/2
अब, d के दोनों मान रखने पर, हम प्राप्त करते हैं,
a = 3 - 4d = 3 - 4(1/2) = 3 - 2 = 1, जब d = 1/2
a = 3 - 4d = 3 - 4(-1/2) = 3+2 = 5, जब d = -1/2
हम जानते हैं, AP के nवें पद का योग है;
एस एन = एन / 2 [2 ए + ( एन -1) डी ]
तो, जब a = 1 और d=1/2
फिर, पहले 16 पदों का योग है;
एस 16 \u003d 16/2 [ 2 + (16-1) 1/2] \u003d 8 (2 + 15/2) \u003d 76
और जब a = 5 और d= -1/2
फिर, पहले 16 पदों का योग है;
एस 16 = 16/2 [2(5)+(16-1)(-1/2)] = 8(5/2)=20
3. एक सीढ़ी 25 सेमी की दूरी पर है। (चित्र 5.7 देखें)। पायदान नीचे की ओर 45 सेमी से लंबाई में समान रूप से कम होकर शीर्ष पर 25 सेमी हो जाते हैं। यदि ऊपर और नीचे के पायदान
अलग-अलग हैं, तो पायदान के लिए आवश्यक लकड़ी की लंबाई क्या है? [संकेत: पायदानों की संख्या = -250/25]।
समाधान:
दिया गया,
सीढ़ी के पायदानों के बीच की दूरी 25cm है।
सीढ़ी के शीर्ष पायदान और निचले पायदान के बीच की दूरी =
= 5/2 × 100cm
= 250 सेमी
अत: चरणों की कुल संख्या = 250/25 + 1 = 11
जैसा कि हम चित्र से देख सकते हैं, सीढ़ी ऊपर से नीचे तक घटते क्रम में चलती है। इस प्रकार, अब हम यह निष्कर्ष निकाल सकते हैं कि AP के क्रम में पायदान घट रहे हैं।
और डंडों के लिए आवश्यक लकड़ी की लंबाई AP श्रेणी के पदों के योग के बराबर होगी।
इसलिए,
पहला पद, a = 45
अंतिम पद, एल = 25
पदों की संख्या, n = 11
अब, जैसा कि हम जानते हैं, nवें पदों का योग बराबर होता है,
एस एन = एन/2(ए+ एल )
एस एन = 11/2(45+25) = 11/2(70) = 385 सेमी
अत: रग्स के लिए आवश्यक लकड़ी की लंबाई 385cm है।
4. एक पंक्ति के घरों को 1 से 49 तक क्रमागत रूप से क्रमांकित किया गया है। दर्शाइए कि x का एक मान इस प्रकार है कि x से पहले के मकानों की संख्या का योग निम्नलिखित घरों की संख्याओं के योग के बराबर है। यह। x का यह मान ज्ञात कीजिए। [संकेत: एसएक्स - 1 = एस49 - एसएक्स]
समाधान:
दिया गया,
पंक्ति के घर 1,2,3,4,5…….49 से संख्याएँ हैं।
इस प्रकार हम देख सकते हैं कि एक पंक्ति में क्रमांकित मकान AP के रूप में हैं।
इसलिए,
पहला पद, a = 1
सामान्य अंतर, डी = 1
मान लें कि x वें घरों की संख्या को इस प्रकार दर्शाया जा सकता है;
AP के nवें पद का योग = n/2[2a+(n-1)d]
x घर से परे घरों की संख्या का योग = S x-1
= (x-1)/2[2(1)+(x-1-1)1]
= (x-1)/2 [2+x-2]
= x(x-1)/2 ………………………………………(i)
दी गई शर्त से, हम लिख सकते हैं,
एस 49 - एस एक्स = {49/2[2(1)+(49-1)1]}-{x/2[2(1)+(x-1)1]}
= 25 (49) - एक्स (एक्स + 1) / 2 …………………………………। (द्वितीय)
दी गई शर्त के अनुसार, eq.(i) और eq(ii) एक दूसरे के बराबर हैं;
इसलिए,
x(x-1)/2 = 25(49) – x(x+1)/2
एक्स = ± 35
जैसा कि हम जानते हैं, घरों की संख्या ऋणात्मक संख्या नहीं हो सकती। अत: x का मान 35 है।
5. फुटबॉल के मैदान में एक छोटी सी छत में 15 सीढ़ियां हैं, जिनमें से प्रत्येक 50 मीटर लंबी है और ठोस कंक्रीट से बनी है। प्रत्येक चरण में 1 4 मीटर की वृद्धि और 1 2 मीटर की एक चाल है। (चित्र 5.8 देखें)। छत बनाने के लिए आवश्यक कंक्रीट की कुल मात्रा की गणना करें। [संकेत : पहला चरण बनाने के लिए आवश्यक कंक्रीट का आयतन = ×1/2 ×50 मी 3। ]
समाधान:
जैसा कि हम दी गई आकृति से देख सकते हैं, पहला चरण आधा मीटर चौड़ा है, दूसरा चरण 1 मीटर चौड़ा है और तीसरा चरण 3/2 मीटर चौड़ा है। इस प्रकार हम समझ सकते हैं कि सीढ़ी की चौड़ाई हर बार ½ मीटर होती है जब ऊंचाई मीटर होती है। और साथ ही, दी गई सीढ़ियों की लंबाई हर समय 50 मीटर है। तो, चरणों की चौड़ाई एक श्रृंखला AP इस प्रकार बनाती है कि;
आधा, 1, 3/2, 2, ……..
चरणों का आयतन = घनाभ का आयतन
= लंबाई × चौड़ाई ऊंचाई
अभी,
पहला चरण बनाने के लिए आवश्यक कंक्रीट का आयतन = ×1/2 ×50 = 25/4
दूसरे चरण के निर्माण के लिए आवश्यक कंक्रीट का आयतन =¼ ×1×50 = 25/2
दूसरे चरण के निर्माण के लिए आवश्यक कंक्रीट का आयतन = ×3/2 ×50 = 75/4
अब, हम देख सकते हैं कि चरणों के निर्माण के लिए आवश्यक कंक्रीट की मात्रा एपी श्रृंखला में हैं;
25/4, 25/2, 75/4…..
इस प्रकार, AP श्रृंखला अवधारणा को लागू करते हुए,
पहला पद, a = 25/4
सामान्य अंतर, d = 25/2 - 25/4 = 25/4
जैसा कि हम जानते हैं, n पदों का योग है;
एस एन = एन/2[2a+(n-1)d] = 15/2(2×(25/4 )+(15/2 -1)25/4)
हल करने पर, हम प्राप्त करते हैं,
एस एन = 15/2 (100)
एस एन = 750
इसलिए, छत बनाने के लिए आवश्यक कंक्रीट की कुल मात्रा 750 मीटर 3 है ।
![[Mathematics - X Notes]* Ncert Mathematics Class - X | Chapter 2. बहुपद In Hindi](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiXsiikGUINI-i6c1s4dNucHy3sSrwZ5ipZub1DIRn2m8MizG6YQHp67wTpnY-Uro7tM1nth6A-DKK6fbD1Q6BiMlkxhpnhXiJCsEpaSlu1dxt64zCXz6V0pMHONB6ytCpGi6p_zpGzsvVCeUK7lwBZW20xPLqWlmJlg7HHRyZKIBRzbpvlqwqZFMCD/w680/20220223_124029.png)
![[Mathematics - X Notes]* Ncert Mathematics Class - X | Chapter 1. वास्तविक संख्या In Hindi](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgEN1UlWgqnFttBsx_dVa5f0uKAFIF9T2fyuc29IOSblF32yR0MPdnNX18wkxJnHX4tv67Ul9h-5YTY98sHsPlbK3bU00gKnl0URKEkIFUGWjA8SAY8TyxpZ9ZZMDS-XYQpag6ymKAn-_zQCamZG4vQ-zGq370Q7nMNNlh6UI4_BSuGGiYmevkFTwAQ/w680/20220223_124029.png)
