NCERT Solutions For Class 10 Math Chapter 10 वृत्त

कक्षा 10 गणित अध्याय 10 के लिए एनसीईआरटी समाधान

NCERT Solutions for Class 10 Maths Chapter 10 वृत्त itselfu में अत्यधिक अनुभवी गणित ट्यूटर्स द्वारा गहन शोध के बाद तैयार किए जाते हैं। यह अध्ययन सामग्री, कक्षा 10 गणित के लिए एनसीईआरटी समाधान आपकी कक्षा 10 के दूसरे सत्र की परीक्षा की तैयारी के लिए बहुत महत्वपूर्ण है। हमने एनसीईआरटी कक्षा 10 गणित की पाठ्यपुस्तक में दिए गए सभी प्रश्नों के उत्तर चरणबद्ध तरीके से प्रदान किए हैं।

कक्षा 10 गणित के लिए एनसीईआरटी समाधान डाउनलोड  करने के लिए स्वतंत्र है और आपकी तैयारी में आसानी और विभिन्न प्रकार के प्रश्नों को हल करने के लिए प्रश्नों को व्यवस्थित रूप से अभ्यास-वार तरीके से व्यवस्थित किया गया है। उच्च अंक प्राप्त करने के लिए, छात्रों को सलाह दी जाती है   कि वे अपनी तैयारी के दौरान इन एनसीईआरटी समाधानों को देखें। 

एनसीईआरटी कक्षा 10 गणित अध्याय 10 - मंडलियों के उत्तर देखें

exercise - 10.1 (पृष्ठ संख्या: 209)

1. एक वृत्त की कितनी स्पर्श रेखाएँ हो सकती हैं?

उत्तर:

एक वृत्त की अनंत स्पर्श रेखाएँ हो सकती हैं । एक वृत्त अनंत बिंदुओं से बना होता है जो एक बिंदु से समान दूरी पर होते हैं। चूँकि वृत्त की परिधि पर अनंत बिंदु होते हैं, उनसे अनंत स्पर्श रेखाएँ खींची जा सकती हैं।

2. रिक्त स्थान भरें:

(i) किसी वृत्त की स्पर्श रेखा उसे …………… बिंदु (बिंदुओं) में काटती है।

(ii) एक वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा ……… कहलाती है।

(iii) एक वृत्त में अधिक से अधिक …………… समानांतर स्पर्श रेखाएँ हो सकती हैं।

(iv) किसी वृत्त और वृत्त की स्पर्श रेखा का उभयनिष्ठ बिंदु ……… कहलाता है।

उत्तर:

(i) किसी वृत्त की स्पर्श रेखा उसे एक बिंदु (बिंदुओं) पर काटती है।

(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा छेदक कहलाती है।

(iii) एक वृत्त की अधिकतम दो समानांतर स्पर्श रेखाएँ हो सकती हैं।

(iv) वृत्त और वृत्त की स्पर्श रेखा का उभयनिष्ठ बिंदु संपर्क बिंदु कहलाता है।

3. 5 सेमी त्रिज्या वाले एक वृत्त के बिंदु P पर स्पर्श रेखा PQ, केंद्र O से होकर जाने वाली एक रेखा से पर मिलती है

एक बिंदु Q ताकि OQ = 12 सेमी. लंबाई पीक्यू है:

(ए) 12 सेमी

(बी) 13 सेमी

(सी) 8.5 सेमी

(डी) √119 सेमी

उत्तर:

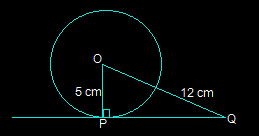
उपरोक्त आकृति में, दिए गए वृत्त के केंद्र से स्पर्श रेखा PQ पर खींची गई रेखा PQ पर लंबवत है।

और इसलिए, ओपी ⊥ पीक्यू

त्रिभुज ΔOPQ में पाइथागोरस प्रमेय का प्रयोग करने पर हमें प्राप्त होता है,

ओक्यू 2 = ओपी 2 + पीक्यू 2

(12) 2 = 5 2 +पीक्यू 2

पीक्यू 2 = 144-25

पीक्यू 2 = 119

पीक्यू = √119 सेमी

तो, विकल्प D यानी √119 सेमी, PQ की लंबाई है।

4. दी गई रेखा के समांतर एक वृत्त और दो रेखाएँ इस प्रकार खींचिए कि उनमें से एक स्पर्श रेखा हो और

अन्य, सर्कल के लिए एक सेकंड।

उत्तर:

उपरोक्त आकृति में, XY और AB दो समानांतर रेखाएँ हैं। रेखा खंड AB बिंदु C पर स्पर्श रेखा है जबकि रेखा खंड XY छेदक है।

---

Exercise 10.2 (पृष्ठ संख्या: 213)

Q.1 से 3 में, सही विकल्प चुनें और औचित्य दें।

1. एक बिंदु Q से, एक वृत्त पर स्पर्श रेखा की लंबाई 24 सेमी है और केंद्र से Q की दूरी 25 सेमी है। वृत्त की त्रिज्या है

(ए) 7 सेमी

(बी) 12 सेमी

(सी) 15 सेमी

(डी) 24.5 सेमी

उत्तर:

सबसे पहले, त्रिभुज के केंद्र O से वृत्त पर एक बिंदु P पर एक लंब खींचिए जो स्पर्शरेखा को स्पर्श कर रहा है। यह रेखा वृत्त की स्पर्श रेखा के लंबवत होगी।

अतः, OP, PQ के लंबवत है अर्थात OP PQ

उपरोक्त आकृति से, यह भी देखा गया है कि △OPQ एक समकोण त्रिभुज है।

दिया जाता है कि

OQ = 25 सेमी और PQ = 24 सेमी

OPQ में पाइथागोरस प्रमेय का प्रयोग करके,

ओक्यू 2 = ओपी 2 + पीक्यू 2

(25) 2 = ओपी 2 + (24) 2

ओपी 2 = 625-576

ओपी 2 = 49

ओपी = 7 सेमी

अतः, विकल्प A अर्थात 7 सेमी दिए गए वृत्त की त्रिज्या है।

2. आकृति 10.11 में, यदि TP और TQ केंद्र 0 वाले एक वृत्त की दो स्पर्श रेखाएँ हैं, जिससे POQ = 110°, तो PTQ बराबर है

(ए) 60 डिग्री

(बी) 70 डिग्री

(सी) 80 डिग्री

(डी) 90 डिग्री

उत्तर:

प्रश्न से, यह स्पष्ट है कि OP वृत्त की स्पर्शरेखा PT की त्रिज्या है और OQ स्पर्शरेखा TQ की त्रिज्या है।

अत: OP ⊥ PT और TQ OQ

OPT = ∠OQT = 90°

अब, चतुर्भुज POQT में, हम जानते हैं कि आंतरिक कोणों का योग 360° . होता है

तो, PTQ+∠POQ+∠OPT+∠OQT = 360°

अब, संबंधित मान रखने पर, हमें प्राप्त होता है,

पीटीक्यू +90°+110°+90° = 360°

पीटीक्यू = 70°

अत: PTQ 70° है जो विकल्प B है।

3. यदि बिंदु P से O केंद्र वाले वृत्त पर स्पर्श रेखाएँ PA और PB एक दूसरे से 80° के कोण पर झुकी हों, तो POA किसके बराबर होगा?

(ए) 50 डिग्री

(बी) 60 डिग्री

(सी) 70 डिग्री

(डी) 80 डिग्री

उत्तर:

पहले दिए गए कथन के अनुसार चित्र बनाइए।

अब, उपरोक्त आरेख में, OA स्पर्शरेखा PA की त्रिज्या है और OB स्पर्शरेखा PB की त्रिज्या है।

तो, OA PA के लंबवत है और OB PB अर्थात OA PA और OB PB पर लंबवत है

अत: OBP = OAP = 90°

अब, चतुर्भुज AOBP में,

सभी आंतरिक कोणों का योग 360° . होगा

अत: ∠AOB+∠OAP+∠OBP+∠APB = 360°

उनके मूल्यों को रखने पर, हम प्राप्त करते हैं,

AOB + 260° = 360°

AOB = 100°

अब, त्रिभुज △OPB और OPA पर विचार करें। यहां,

एपी = बीपी (चूंकि एक बिंदु से स्पर्शरेखा हमेशा बराबर होती है)

OA = OB (वृत्त की त्रिज्याएँ कौन-सी हैं)

OP = OP (यह उभयनिष्ठ पक्ष है)

अब, हम कह सकते हैं कि SSS सर्वांगसमता का उपयोग करते हुए त्रिभुज OPB और OPA समरूप हैं।

ओपीबी ओपीए

अत: POB = POA

AOB = POA+∠POB

2 (∠POA) = AOB

संबंधित मान रखने पर, हम प्राप्त करते हैं,

=>∠पीओए = 100°/2 = 50°

कोण POA 50° है, विकल्प A सही विकल्प है।

4. सिद्ध कीजिए कि एक वृत्त के व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं।

उत्तर:

सबसे पहले, एक वृत्त खींचिए और दो बिंदुओं A और B को इस प्रकार जोड़िए कि AB वृत्त का व्यास बन जाए। अब, बिंदु A और B पर क्रमशः दो स्पर्श रेखाएँ PQ और RS खींचिए।

अब, दोनों त्रिज्याएँ अर्थात AO और OB स्पर्शरेखाओं पर लंबवत हैं।

अत: OB RS पर लम्ब है और OA PQ पर लम्ब है

अत: OAP = OAQ = OBR = OBS = 90°

उपरोक्त आकृति से, कोण OBR और OAQ एकांतर आंतरिक कोण हैं।

साथ ही, OBR = OAQ और ∠OBS = OAP (चूंकि वे एकांतर आंतरिक कोण भी हैं)

अतः, यह कहा जा सकता है कि रेखा PQ और रेखा RS एक दूसरे के समानांतर होगी। (इसलिए सिद्ध)।

5. सिद्ध कीजिए कि वृत्त पर स्पर्श रेखा के संपर्क बिंदु पर लम्ब केंद्र से होकर जाता है।

समाधान:

मान लीजिए AB, O वाले वृत्त पर बिंदु P पर खींची गई स्पर्श रेखा है। 

यदि संभव हो तो, मान लीजिए कि PQ, AB पर लम्ब है, O से होकर नहीं जाता है।

ओपी में शामिल हों।

चूँकि एक वृत्त पर एक बिंदु पर स्पर्शरेखा बिंदु के माध्यम से त्रिज्या के लंबवत होती है।

इसलिए  , AB OP  ⇒           ⇒           OPB = 90 o

साथ ही ,  QPB = 90 o             $\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">बी</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">आप</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">सी</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">हे</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">एन</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">एस</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">टी</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">आर</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">तुम</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">सी</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">टी</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">मैं</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">हे</span></span>}\mathrm{<span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;"><span\; style="box-sizing:\; border-box;\; vertical-align:\; inherit;">एन</span></span>}$

इसलिए,   QPB =  OPB , जो संभव नहीं है क्योंकि एक भाग पूर्ण के बराबर नहीं हो सकता।

इस प्रकार, यह हमारे अनुमान के विपरीत है।

अत: वृत्त की स्पर्श रेखा के संपर्क बिंदु पर लम्ब केंद्र से होकर गुजरता है।

6. वृत्त के केंद्र से 5 सेमी की दूरी पर एक बिंदु A से स्पर्श रेखा की लंबाई 4 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए।

उत्तर:

नीचे दिखाए अनुसार आरेख बनाएं।

यहाँ, AB एक बिंदु A से वृत्त पर खींची गई स्पर्श रेखा है।

अत: त्रिज्या OB AB पर लंबवत होगी अर्थात OB AB

हम जानते हैं, OA = 5 सेमी और AB = 4 सेमी

अब, ABO में,

OA 2 =AB 2 +BO 2 (पाइथागोरस प्रमेय का प्रयोग करके)

5 2 = 4 2 +बीओ 2

बीओ 2 = 25-16

बीओ 2 = 9

बीओ = 3

अतः दिए गए वृत्त की त्रिज्या अर्थात BO 3 सेमी है।

7. दो संकेंद्रित वृत्तों की त्रिज्याएँ 5 सेमी और 3 सेमी हैं। बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती है।

उत्तर:

केंद्र O के साथ दो संकेंद्रित वृत्त खींचिए। अब, बड़े वृत्त में एक जीवा AB खींचिए जो छोटे वृत्त को बिंदु P पर स्पर्श करती है जैसा कि नीचे दिए गए चित्र में दिखाया गया है।

उपरोक्त आरेख से, AB छोटे वृत्त पर बिंदु P पर स्पर्श रेखा है।

ओपी ⊥ एबी

त्रिभुज OPA में पाइथागोरस प्रमेय का प्रयोग करते हुए,

ओए 2 = एपी 2 +ओपी 2

5 2 = एपी 2 +3 2

एपी 2 = 25-9

एपी = 4

अब, OP AB के रूप में,

चूँकि वृत्त के केंद्र से लम्ब जीवा को समद्विभाजित करता है, AP, PB के बराबर होगा

अत: AB = 2AP = 2×4 = 8 सेमी

अत: बड़े वृत्त की जीवा की लंबाई 8 सेमी है।

8. एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है (देखिए आकृति 10.12)। सिद्ध कीजिए कि AB + CD = AD + BC

उत्तर:

दिया गया आंकड़ा है:

इस आंकड़े से हम कुछ बिंदुओं पर निष्कर्ष निकाल सकते हैं जो इस प्रकार हैं:

(i) डीआर = डीएस

(ii) बीपी = बीक्यू

(iii) एपी = एएस

(iv) सीआर = सीक्यू

चूँकि वे क्रमशः बिंदु D, B, A और C से वृत्त पर स्पर्श रेखाएँ हैं।

अब, उपरोक्त समीकरणों के LHS और RHS को जोड़ने पर, हमें प्राप्त होता है,

डीआर+बीपी+एपी+सीआर = डीएस+बीक्यू+एएस+सीक्यू

उन्हें पुनर्व्यवस्थित करने से हम प्राप्त करते हैं,

(डीआर+सीआर) + (बीपी+एपी) = (सीक्यू+बीक्यू) + (डीएस+एएस)

सरलीकरण करके,

एडी+बीसी=सीडी+एबी

9. आकृति 10.13 में, XY और X′Y′ केंद्र O वाले एक वृत्त की दो समानांतर स्पर्श रेखाएँ हैं और संपर्क बिंदु C वाली एक अन्य स्पर्श रेखा AB, XY को A और X′Y′ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि AOB = 90 °.

उत्तर:

पाठ्यपुस्तक में दिए गए चित्र से OC को मिलाइए। अब, आरेख इस प्रकार होगा-

अब त्रिभुज △OPA और △OCA SSS सर्वांगसमता का उपयोग करते हुए समान हैं:

(i) OP = OC वे एक ही वृत्त की त्रिज्याएँ हैं

(ii) AO = AO यह उभयनिष्ठ पक्ष है

(iii) AP = AC ये बिंदु A से स्पर्श रेखाएँ हैं

तो, OPA OCA

इसी तरह,

OQB OCB

इसलिए,

POA = COA … (समीकरण i)

और, QOB = COB … (समीकरण ii)

चूँकि रेखा POQ एक सीधी रेखा है, इसे वृत्त का व्यास माना जा सकता है।

अत: POA +∠COA +∠COB +∠QOB = 180°

अब, समीकरण (i) और समीकरण (ii) से हम प्राप्त करते हैं,

2∠COA+2∠COB = 180°

COA+∠COB = 90°

AOB = 90°

10. सिद्ध कीजिए कि किसी बाह्य बिंदु से वृत्त पर खींची गई दो स्पर्श रेखाओं के बीच का कोण, केंद्र पर संपर्क बिंदुओं को मिलाने वाले रेखाखंड द्वारा अंतरित कोण का संपूरक होता है।

उत्तर:

सबसे पहले, केंद्र O वाला एक वृत्त बनाएं। एक बाहरी बिंदु P चुनें और बिंदु A और बिंदु B पर क्रमशः दो स्पर्श रेखाएँ PA और PB खींचे। अब, A और B को मिलाकर AB इस प्रकार बनाएं कि वह वृत्त के केंद्र पर AOB को घटाए। आरेख इस प्रकार है:

उपरोक्त आरेख से, यह देखा गया है कि रेखा खंड OA और PA लंबवत हैं।

अत: OAP = 90°

इसी प्रकार, रेखा खंड OB PB और इसलिए, OBP = 90°

अब, चतुर्भुज OAPB में,

APB+∠OAP +∠PBO +∠BOA = 360° (क्योंकि सभी आंतरिक कोणों का योग 360° होगा)

हमें प्राप्त होने वाले मान डालने से,

APB + 180° + BOA = 360°

अत: APB + BOA = 180° (इसलिए सिद्ध हुआ)।

11. सिद्ध कीजिए कि एक वृत्त के परिगत समांतर चतुर्भुज एक समचतुर्भुज होता है।

उत्तर:

एक समांतर चतुर्भुज ABCD पर विचार करें जो O केंद्र वाले एक वृत्त के परिगत है। अब, चूँकि ABCD एक समांतर चतुर्भुज है, AB = CD और BC = AD है।

उपरोक्त आकृति से यह देखा जा सकता है कि,

(i) डीआर = डीएस

(ii) बीपी = बीक्यू

(iii) सीआर = सीक्यू

(iv) एपी = एएस

ये क्रमशः D, B, C और A पर वृत्त की स्पर्श रेखाएँ हैं।

इन सभी को जोड़ने पर हमें प्राप्त होता है,

डीआर+बीपी+सीआर+एपी = डीएस+बीक्यू+सीक्यू+एएस

उन्हें पुनर्व्यवस्थित करने से हम प्राप्त करते हैं,

(बीपी+एपी)+(डीआर+सीआर) = (सीक्यू+बीक्यू)+(डीएस+एएस)

उन्हें पुन: व्यवस्थित करने पर हमें प्राप्त होता है,

एबी+सीडी = बीसी+एडी

अब, क्योंकि AB = CD और BC = AD, उपरोक्त समीकरण बन जाता है

2AB = 2BC

एबी = बीसी

चूँकि AB = BC = CD = DA, यह कहा जा सकता है कि ABCD एक समचतुर्भुज है।

12. 4 सेमी त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि खण्ड BD और DC, जिनमें BC को संपर्क बिंदु D से विभाजित किया गया है, की लंबाई क्रमशः 8 सेमी और 6 सेमी है (देखिए आकृति 10.14)। भुजाएँ AB और AC ज्ञात कीजिए।

उत्तर:

दिया गया आंकड़ा इस प्रकार है:

त्रिभुज ABC पर विचार करें,

हम जानते हैं कि एक ही बिंदु से वृत्त पर खींची गई किन्हीं दो स्पर्श रेखाओं की लंबाई बराबर होती है।

इसलिए,

(i) CF = सीडी = 6 सेमी

(ii) बीई = बीडी = 8 सेमी

(iii) एई = एएफ = एक्स

अब, यह देखा जा सकता है कि,

(i) एबी = ईबी+एई = 8+x

(ii) सीए = सीएफ+एफए = 6+ x

(iii) बीसी = डीसी+बीडी = 6+8 = 14

अब अर्ध परिमाप "s" की गणना इस प्रकार की जाएगी

2s = AB+CA+BC

संबंधित मान डालने से हमें प्राप्त होता है,

2s = 28+2 x

एस = 14+ एक्स

इसे हल करने से हमें प्राप्त होता है,

= (14+ x )48 x ……… (i)

पुनः, ABC का क्षेत्रफल = 2 × (△AOF + △COD + △DOB) का क्षेत्रफल

= 2×[(½×OF×AF)+(½×CD×OD)+(½×DB×OD)]

= 2×½(4 x +24+32) = 56+4 x ……………..(ii)

अब (i) और (ii) से हम पाते हैं,

(14+ x )48 x = 56+4 x

अब, दोनों पक्षों को चौकोर करें,

48 x (14+ x ) = (56+4 x ) 2

48 x = [4(14+x)] 2 /(14+ x )

48 x = 16(14+ x )

48 x = 224+16 x

32 x = 224

एक्स = 7 सेमी

अत: AB = 8+x

यानी एबी = 15 सेमी

और, सीए = x+6 =13 सेमी।

13. सिद्ध कीजिए कि वृत्त के परिगत एक चतुर्भुज की सम्मुख भुजाएँ वृत्त के केंद्र पर संपूरक कोण अंतरित करती हैं।

उत्तर:

पहले एक चतुर्भुज ABCD खीचें जो एक वृत्त को उसके केंद्र O के साथ इस प्रकार परिबद्ध करेगा कि वह बिंदु P, Q, R और S पर वृत्त को स्पर्श करता है। अब, ABCD के शीर्षों को मिलाने के बाद हमें निम्नलिखित आकृति प्राप्त होती है:

अब, त्रिभुजों OAP और OAS पर विचार करें,

AP = AS (वे एक ही बिंदु A से स्पर्श रेखाएँ हैं)

OA = OA (यह उभयनिष्ठ पक्ष है)

OP = OS (वे वृत्त की त्रिज्याएँ हैं)

अतः, SSS सर्वांगसमता से OAP ≅ OAS

अत: POA = AOS

जिसका अर्थ है कि∠1 = ∠8

इसी तरह, अन्य कोण होंगे,

4 = ∠5

2 = ∠3

6 = ∠7

अब इन कोणों को जोड़ने पर हमें प्राप्त होता है,

∠1+∠2+∠3 +∠4 +∠5+∠6+∠7+∠8 = 360°

अब पुनर्व्यवस्थित करके,

(∠1+∠8)+(∠2+∠3)+(∠4+∠5)+(∠6+∠7) = 360°

2∠1+2∠2+2∠5+2∠6 = 360°

2 को समान मानकर हल करने पर हमें प्राप्त होता है,

(∠1+∠2)+(∠5+∠6) = 180°

अत: ∠AOB+∠COD = 180°

इसी प्रकार, यह सिद्ध किया जा सकता है कि BOC+∠DOA = 180°

इसलिए, किसी भी चतुर्भुज की सम्मुख भुजाएँ, जो किसी दिए गए वृत्त के परिगत हैं, वृत्त के केंद्र पर संपूरक कोण अंतरित करेंगी।