एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 4
NCERT Solutions Class 10 Maths Chapter 4 द्विघात समीकरणों में कक्षा 10 गणित NCERT पाठ्यपुस्तक में दूसरे सत्र की परीक्षा की तैयारी के लिए प्रदान की गई समस्याओं के सभी समाधान शामिल हैं। प्रत्येक खंड के प्रश्नों को विषय विशेषज्ञों द्वारा तैयार किया जाता है और सटीक रूप से हल किया जाता है। कक्षा 10 के लिए एनसीईआरटी समाधान छात्रों के सभी प्रश्नों के लिए एक विस्तृत और चरण-दर-चरण मार्गदर्शिका है। यदि कोई परीक्षा में अच्छा स्कोर करना चाहता है तो अध्याय में मौजूद अभ्यासों को पूरी ईमानदारी से निपटाया जाना चाहिए। गणित एक ऐसा विषय है जिसके लिए अच्छी समझ और बहुत अभ्यास की आवश्यकता होती है। समस्याओं को आसानी से हल करने के टिप्स और ट्रिक्स भी यहां दिए गए हैं। चर x में एक द्विघात समीकरण ax 2 + bx + c = 0 के रूप का एक समीकरण है, जहाँ a, b, c वास्तविक संख्याएँ हैं, a 0। अर्थात्, ax2 + bx + c = 0, a 0 द्विघात समीकरण का मानक रूप कहलाता है।
हमारे आस-पास कई स्थितियों में द्विघात समीकरण उत्पन्न होते हैं। इसलिए, छात्रों को कक्षा 10 के द्वितीय सत्र की परीक्षाओं में उत्कृष्टता प्राप्त करने के लिए 2012-22 के नवीनतम सीबीएसई पाठ्यक्रम के इस अध्याय से संबंधित अवधारणाओं को सीखने पर विशेष ध्यान देना चाहिए। एनसीईआरटी समाधान छात्रों को इन अवधारणाओं को सीखने के साथ-साथ स्वयं का मूल्यांकन करने में मदद करते हैं। इन समाधानों का बार-बार अभ्यास करने से छात्रों को अपनी कमियों को दूर करने में मदद मिलेगी। गणित में या तो सही उत्तर होता है या गलत। इसलिए, पूर्ण अंक प्राप्त करने के लिए प्रश्नों को हल करते समय ध्यान केंद्रित करना अनिवार्य है।
एनसीईआरटी कक्षा 10 गणित अध्याय 4 - द्विघात समीकरण के उत्तर देखें
Exercise - 4.1 पृष्ठ: 73
1. जाँच कीजिए कि क्या निम्नलिखित द्विघात समीकरण हैं:
(i) (एक्स + 1) 2 = 2 (एक्स - 3)
(ii) x 2 - 2x = (-2) (3 - x)
(iii) (x - 2)(x + 1) = (x - 1)(x + 3)
(iv) (x - 3)(2x +1) = x(x + 5)
(v) (2x - 1)(x - 3) = (x + 5)(x - 1)
(vi) x 2 + 3x + 1 = (x - 2) 2
(vii) (x + 2) 3 = 2x (x 2 - 1)
(viii) x 3 - 4x 2 - x + 1 = (x - 2) 3
समाधान:
(मैंने दे दिया,
(एक्स + 1) 2 = 2 (एक्स - 3)
(a+b) 2 = a 2 +2ab+b 2 . के लिए सूत्र का उपयोग करके
x 2 + 2x + 1 = 2x - 6
⇒ एक्स 2 + 7 = 0
चूँकि उपरोक्त समीकरण ax 2 + bx + c = 0 के रूप में है।
अतः दिया गया समीकरण द्विघात समीकरण है।
(ii) दिया गया है, x 2 - 2x = (-2) (3 - x)
⇒ एक्स 2 - 2x = -6 + 2x
एक्स 2 - 4x + 6 = 0
चूँकि उपरोक्त समीकरण ax 2 + bx + c = 0 के रूप में है।
अतः दिया गया समीकरण द्विघात समीकरण है।
(iii) दिया गया है, (x - 2)(x + 1) = (x - 1)(x + 3)
गुणन द्वारा
x 2 - x - 2 = x 2 + 2x - 3
3x - 1 = 0
चूँकि उपरोक्त समीकरण ax 2 + bx + c = 0 के रूप में नहीं है।
अतः दिया गया समीकरण द्विघात समीकरण नहीं है।
(iv) दिया गया है, (x - 3)(2x +1) = x(x + 5)
गुणन द्वारा
2x 2 - 5x - 3 = x 2 + 5x
x 2 - 10x - 3 = 0
चूँकि उपरोक्त समीकरण ax 2 + bx + c = 0 के रूप में है।
अतः दिया गया समीकरण द्विघात समीकरण है।
(v) दिया गया है, (2x - 1)(x - 3) = (x + 5)(x - 1)
गुणन द्वारा
⇒ 2x 2 - 7x + 3 = x 2 + 4x - 5
एक्स 2 - 11x + 8 = 0
चूँकि उपरोक्त समीकरण ax 2 + bx + c = 0 के रूप में है।
अतः दिया गया समीकरण द्विघात समीकरण है।
(vi) दिया गया है, x 2 + 3x + 1 = (x - 2) 2
(ab) 2 =a 2 -2ab+b 2 . के लिए सूत्र का उपयोग करके
x 2 + 3x + 1 = x 2 + 4 - 4x
⇒ 7x - 3 = 0
चूँकि उपरोक्त समीकरण ax 2 + bx + c = 0 के रूप में नहीं है।
अतः दिया गया समीकरण द्विघात समीकरण नहीं है।
(vii) दिया गया है, (x + 2) 3 = 2x (x 2 - 1)
(a+b) 3 = a 3 +b 3 +3ab(a+b) के लिए सूत्र का उपयोग करके
x 3 + 8 + x 2 + 12x = 2x 3 - 2x
x 3 + 14x - 6x 2 - 8 = 0
चूँकि उपरोक्त समीकरण ax 2 + bx + c = 0 के रूप में नहीं है।
अतः दिया गया समीकरण द्विघात समीकरण नहीं है।
(viii) दिया गया है, x 3 - 4x 2 - x + 1 = (x - 2) 3
(ab) 3 = a 3 -b 3 -3ab(ab) के लिए सूत्र का उपयोग करके
x 3 - 4x 2 - x + 1 = x 3 - 8 - 6x 2 + 12x
2x 2 - 13x + 9 = 0
चूँकि उपरोक्त समीकरण ax 2 + bx + c = 0 के रूप में है।
अतः दिया गया समीकरण द्विघात समीकरण है।
2. निम्नलिखित स्थितियों को द्विघात समीकरणों के रूप में निरूपित करें:
( i ) एक आयताकार भूखंड का क्षेत्रफल 528 m2 है । भूखंड की लंबाई (मीटर में) इसकी चौड़ाई के दोगुने से एक अधिक है। हमें भूखंड की लंबाई और चौड़ाई खोजने की जरूरत है।
(ii) दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 306 है। हमें पूर्णांक ज्ञात करने होंगे।
(iii) रोहन की माँ उससे 26 वर्ष बड़ी है। अब से 3 वर्ष बाद उनकी आयु (वर्षों में) का गुणनफल 360 होगा। हम रोहन की वर्तमान आयु ज्ञात करना चाहेंगे।
(iv) एक ट्रेन एक समान गति से 480 किमी की दूरी तय करती है। अगर गति 8 किमी/घंटा कम होती, तो यह लग जाता
समाधान:
(i) आइए विचार करें,
आयताकार भूखंड की चौड़ाई = x m
अत: भूखंड की लंबाई = (2x + 1) मी.
जैसा कि हम जानते हैं,
आयत का क्षेत्रफल = लंबाई × चौड़ाई = 528 मीटर 2
प्लॉट की लंबाई और चौड़ाई का मान सूत्र में रखने पर, हम प्राप्त करते हैं,
(2x + 1) × x = 528
⇒ 2x 2 + x =528
⇒ 2x 2 + x - 528 = 0
इसलिए, भूखंड की लंबाई और चौड़ाई, द्विघात समीकरण, 2x 2 + x - 528 = 0 को संतुष्ट करती है, जो गणितीय रूप से समस्या का आवश्यक प्रतिनिधित्व है।
(ii) आइए विचार करें,
पहली पूर्णांक संख्या = x
अत: अगला क्रमागत धनात्मक पूर्णांक = x + 1 . होगा
दो क्रमागत पूर्णांकों का गुणनफल = x × (x +1) = 306
एक्स 2 + एक्स = 306
एक्स 2 + एक्स - 306 = 0
इसलिए, दो पूर्णांक x और x+1, द्विघात समीकरण, x 2 + x - 306 = 0 को संतुष्ट करते हैं, जो गणितीय रूप से समस्या का आवश्यक प्रतिनिधित्व है।
(iii) आइए विचार करें,
रोहन की आयु = x वर्ष
इसलिए, दिए गए प्रश्न के अनुसार,
रोहन की माँ की आयु = x + 26
3 साल बाद,
रोहन की आयु = x + 3
रोहन की माता की आयु होगी = x + 26 + 3 = x + 29
3 वर्ष बाद उनकी आयु का गुणनफल 360 के बराबर होगा, जैसे
(एक्स + 3) (एक्स + 29) = 360
⇒ x 2 + 29x + 3x + 87 = 360
x 2 + 32x + 87 - 360 = 0
x 2 + 32x - 273 = 0
अतः रोहन और उसकी माँ की आयु द्विघात समीकरण x 2 + 32x - 273 = 0 को संतुष्ट करती है, जो गणितीय रूप से समस्या का आवश्यक निरूपण है।
(iv) आइए विचार करें,
ट्रेन की गति = x किमी/घंटा
और
480 किमी की यात्रा में लगने वाला समय = 480/x किमी/घंटा
दूसरी शर्त के अनुसार, ट्रेन की गति = ( x - 8) किमी/घंटा
साथ ही दिया गया है कि समान दूरी तय करने में ट्रेन को 3 घंटे का समय लगेगा.
इसलिए, 480 किमी की यात्रा करने में लिया गया समय = (480/x)+3 किमी/घंटा
जैसा कि हम जानते हैं,
गति × समय = दूरी
इसलिए,
( एक्स - 8)(480/ एक्स )+ 3 = 480
480 + 3 x - 3840/ x - 24 = 480
3 एक्स - 3840/ एक्स = 24
एक्स 2 - 8 एक्स - 1280 = 0
इसलिए, ट्रेन की गति, द्विघात समीकरण x 2 - 8 x - 1280 = 0 को संतुष्ट करती है, जो गणितीय रूप से समस्या का आवश्यक प्रतिनिधित्व है।
Exercise - 4.2 पृष्ठ: 76
1. गुणनखंडन द्वारा निम्नलिखित द्विघात समीकरणों के मूल ज्ञात कीजिए:
(i) x 2 - 3x - 10 = 0
(ii) 2x 2 + x - 6 = 0
(iii) 2 x 2 + 7x + 5√2 = 0
(iv) 2x 2 - x +1/8 = 0
(v) 100x 2 - 20x + 1 = 0
समाधान:
(i) दिया गया है, x 2 - 3 x - 10 = 0
एलएचएस लेना,
=> x 2 - 5 x + 2 x - 10
=> एक्स ( एक्स - 5) + 2 ( एक्स - 5)
=>( x - 5)( x + 2)
इस समीकरण के मूल, x 2 - 3 x - 10 = 0, x के वे मान हैं जिनके लिए ( x - 5)( x + 2) = 0
इसलिए, x - 5 = 0 या x + 2 = 0
=> x = 5 या x = -2
(ii) दिया गया है, 2 x 2 + x - 6 = 0
एलएचएस लेना,
=> 2 x 2 + 4 x - 3 x - 6
=> 2 एक्स ( एक्स + 2) - 3 ( एक्स + 2)
=> ( एक्स + 2)(2 एक्स – 3)
इस समीकरण के मूल, 2 x 2 + x - 6=0, x के वे मान हैं जिनके लिए ( x x + 2)(2 x - 3) = 0
इसलिए, x + 2 = 0 या 2 x - 3 = 0
=> x = -2 या x = 3/2
(iii) √2 x 2 + 7 x + 5√2=0
एलएचएस लेना,
=> 2 x 2 + 5 x + 2 x + 5√2
=> x (√2 x + 5) + √2(√2 x + 5)= (√2 x + 5)( x + √2)
इस समीकरण की जड़ें, 2 x 2 + 7 x + 5√2=0 x के मान हैं जिसके लिए (√2 x + 5)( x + √2) = 0
इसलिए, 2 x + 5 = 0 या x + √2 = 0
=> x = -5/√2 या x = -√2
(iv) 2 x 2 - x +1/8 = 0
एलएचएस लेना,
=1/8 (16 x 2 - 8 x + 1)
= 1/8 (16 x 2 - 4 x -4 x + 1)
= 1/8 (4 x (4 x - 1) -1(4 x - 1))
= 1/8 (4 x - 1) 2
इस समीकरण के मूल, 2 x 2 - x + 1/8 = 0, x के वे मान हैं जिनके लिए (4 x - 1) 2 = 0
इसलिए, (4 x - 1) = 0 या (4 x - 1) = 0
एक्स = 1/4 या एक्स = 1/4
(v) दिया गया है, 100x 2 - 20x + 1=0
एलएचएस लेना,
= 100x 2 - 10x - 10x + 1
= 10x(10x - 1) -1(10x - 1)
= (10x - 1) 2
इस समीकरण के मूल, 100x 2 - 20x + 1=0, x के वे मान हैं जिनके लिए (10x - 1) 2 = 0
(10x - 1) = 0 या (10x - 1) = 0
x = 1/10 या x = 1/10
2. उदाहरण 1 में दी गई समस्याओं को हल कीजिए।
निम्नलिखित स्थितियों को गणितीय रूप से निरूपित करें:
(i) जॉन और जिवंती के पास मिलाकर 45 कंचे हैं। उनमें से प्रत्येक ने 5 कंचे खो दिए, और अब उनके पास जितने कंचे हैं उनकी संख्या का गुणनफल 124 है। हम यह पता लगाना चाहेंगे कि उन्हें कितने कंचों से शुरुआत करनी थी।
(ii) एक कुटीर उद्योग एक दिन में निश्चित संख्या में खिलौनों का उत्पादन करता है। प्रत्येक खिलौने की उत्पादन लागत (रुपये में) एक दिन में उत्पादित खिलौनों की संख्या से 55 घटा पाया गया। एक विशेष दिन, उत्पादन की कुल लागत ₹ 750 थी। हम उस दिन उत्पादित खिलौनों की संख्या ज्ञात करना चाहेंगे।
समाधान:
(i) मान लीजिए, जॉन के पास जितने कंचों की संख्या है = x ।
इसलिए, जिवंती में संगमरमर की संख्या = 45 - x . है
प्रत्येक में 5 कंचे खोने के बाद,
जॉन के पास जितने कंचों की संख्या है = x - 5
जिवंती में संगमरमर की संख्या = 45 - x - 5 = 40 - x . है
दिया गया है कि उनके कंचों का गुणनफल 124 है।
( x - 5) (40 - x ) = 124
x 2 - 45 x + 324 = 0
x 2 - 36 x - 9 x + 324 = 0
एक्स ( एक्स - 36) -9 ( एक्स - 36) = 0
( x - 36)( x - 9) = 0
इस प्रकार, हम कह सकते हैं,
एक्स - 36 = 0 या एक्स - 9 = 0
x = 36 या x = 9
इसलिए,
यदि, जॉन के कंचे = 36,
तब, जिवंती के कंचे = 45 - 36 = 9
और यदि जॉन के कंचे = 9,
तब, जिवंती के कंचे = 45 - 9 = 36
(ii) मान लीजिए, एक दिन में उत्पादित खिलौनों की संख्या x है ।
इसलिए, प्रत्येक खिलौने की उत्पादन लागत = रु (55 - x )
दिया गया है, खिलौनों के उत्पादन की कुल लागत = 750 . रुपये
एक्स (55 - एक्स ) = 750
एक्स 2 - 55 एक्स + 750 = 0
x 2 - 25 x - 30 x + 750 = 0
एक्स ( एक्स - 25) -30 ( एक्स - 25) = 0
( एक्स - 25) ( एक्स - 30) = 0
इस प्रकार, या तो x - 25 = 0 या x – 30 = 0
एक्स = 25 या एक्स = 30
अत: एक दिन में उत्पादित खिलौनों की संख्या 25 या 30 होगी।
3. दो संख्याएँ ज्ञात कीजिए जिनका योग 27 और गुणनफल 182 है।
समाधान:
मान लीजिए, पहली संख्या x है और दूसरी संख्या 27 - x है।
इसलिए, दो संख्याओं का गुणनफल
एक्स (27 - एक्स) = 182
x 2 - 27x - 182 = 0
x 2 - 13x - 14x + 182 = 0
एक्स (एक्स - 13) -14 (एक्स - 13) = 0
(एक्स - 13) (एक्स -14) = 0
इस प्रकार, या तो x = -13 = 0 या x - 14 = 0
एक्स = 13 या एक्स = 14
इसलिए, यदि पहली संख्या = 13, तो दूसरी संख्या = 27 - 13 = 14
और यदि पहली संख्या = 14, तो दूसरी संख्या = 27 - 14 = 13
अत: संख्याएँ 13 और 14 हैं।
4. दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 365 है।
समाधान:
मान लीजिए, दो क्रमागत धनात्मक पूर्णांक x और x + 1 हैं।
इसलिए, दिए गए प्रश्नों के अनुसार,
एक्स 2 + ( एक्स + 1) 2 = 365
एक्स 2 + एक्स 2 + 1 + 2 एक्स = 365
2 x 2 + 2x - 364 = 0
एक्स 2 + एक्स - 182 = 0
x 2 + 14 x - 13 x - 182 = 0
एक्स ( एक्स + 14) -13 ( एक्स + 14) = 0
( एक्स + 14)( एक्स – 13) = 0
इस प्रकार, या तो x + 14 = 0 या x - 13 = 0,
x = – 14 या x = 13
चूंकि, पूर्णांक धनात्मक हैं, इसलिए x केवल 13 हो सकता है।
एक्स + 1 = 13 + 1 = 14
इसलिए, दो क्रमागत धनात्मक पूर्णांक 13 और 14 होंगे।
5. एक समकोण त्रिभुज की ऊंचाई उसके आधार से 7 सेमी कम है। यदि कर्ण 13 सेमी है, तो अन्य दो भुजाएँ ज्ञात कीजिए।
समाधान:
मान लीजिए, समकोण त्रिभुज का आधार x सेमी है।
दिया गया है, समकोण त्रिभुज की ऊँचाई = (x - 7) cm
पाइथागोरस प्रमेय से, हम जानते हैं,
आधार 2 + ऊंचाई 2 = कर्ण 2
∴ x 2 + (x - 7) 2 = 13 2
x 2 + x 2 + 49 - 14x = 169
⇒ 2x 2 - 14x - 120 = 0
⇒ एक्स 2 - 7x - 60 = 0
x 2 - 12x + 5x - 60 = 0
एक्स (एक्स - 12) + 5 (एक्स - 12) = 0
(एक्स - 12) (एक्स + 5) = 0
इस प्रकार, या तो x – 12 = 0 या x + 5 = 0,
x = 12 या x = - 5
चूँकि भुजाएँ ऋणात्मक नहीं हो सकतीं, x केवल 12 हो सकता है।
अत: दिए गए त्रिभुज का आधार 12 सेमी है और इस त्रिभुज की ऊंचाई (12 - 7) सेमी = 5 सेमी होगी।
6. एक कुटीर उद्योग एक दिन में एक निश्चित संख्या में मिट्टी के बर्तनों का उत्पादन करता है। एक विशेष दिन यह देखा गया कि प्रत्येक वस्तु की उत्पादन लागत (रुपयों में) उस दिन उत्पादित वस्तुओं की संख्या के दोगुने से 3 अधिक थी। यदि उस दिन उत्पादन की कुल लागत 90 रुपये थी, तो उत्पादित वस्तुओं की संख्या और प्रत्येक वस्तु की लागत ज्ञात कीजिए।
समाधान:
मान लीजिए, उत्पादित वस्तुओं की संख्या x है ।
इसलिए, प्रत्येक वस्तु की उत्पादन लागत = रुपये (2 x + 3)
दिया गया है, उत्पादन की कुल लागत 90 . रुपये है
एक्स (2 एक्स + 3 ) = 90
2 x 2 + 3 x - 90 = 0
2 x 2 + 15 x -12 x - 90 = 0
एक्स (2 एक्स + 15) -6 (2 एक्स + 15) = 0
(2 x + 15)( x - 6) = 0
इस प्रकार, या तो 2 x + 15 = 0 या x - 6 = 0
एक्स = -15/2 या एक्स = 6
चूंकि उत्पादित वस्तुओं की संख्या केवल एक सकारात्मक पूर्णांक हो सकती है, इसलिए x केवल 6 हो सकता है।
अत: उत्पादित वस्तुओं की संख्या = 6
प्रत्येक वस्तु का मूल्य = 2 × 6 + 3 = 15 रुपये।
Exercise - 4.3 पृष्ठ: 87
1. निम्नलिखित द्विघात समीकरणों के मूल, यदि वे मौजूद हैं, वर्ग पूर्ण करने की विधि द्वारा ज्ञात कीजिए:
(i) 2 x 2 - 7 x +3 = 0
(ii) 2 x 2 + x - 4 = 0
(iii) 4 x 2 + 4√3 x + 3 = 0
(iv) 2 x 2 + x + 4 = 0
समाधान:
(i) 2 x 2 - 7 x + 3 = 0
2 x 2 - 7 x = - 3
दोनों पक्षों में 2 से भाग देने पर, हम प्राप्त करते हैं
⇒ एक्स 2 -7x/2 = -3/2
⇒ x 2 -2 × x ×7/4 = -3/2
समीकरण के दोनों पक्षों में (7/4) 2 जोड़ने पर, हम प्राप्त करते हैं
(x) 2 -2×x×7/4 +(7/4) 2 = (7/4) 2 -3/2
(x-7/4) 2 = (49/16) - (3/2)
(x-7/4) 2 = 25/16
(x-7/4) 2 = ±5/4
⇒ एक्स = 7/4 ± 5/4
x = 7/4 + 5/4 या x = 7/4 - 5/4
एक्स = 12/4 या एक्स = 2/4
एक्स = 3 या एक्स = 1/2
(ii) 2x 2 + x - 4 = 0
2x 2 + x = 4
समीकरण के दोनों पक्षों को 2 से भाग देने पर, हम प्राप्त करते हैं
⇒ x 2 +x/2 = 2
अब समीकरण के दोनों पक्षों में (1/4) 2 जोड़ने पर, हम प्राप्त करते हैं,
(एक्स) 2 + 2 × एक्स × 1/4 + (1/4) 2 = 2 + (1/4) 2
(एक्स + 1/4) 2 = 33/16
⇒ एक्स + 1/4 = ± √33/4
एक्स = ± 33/4 - 1/4
⇒ एक्स = (± √33-1) / 4
इसलिए, या तो x = (√33-1)/4 या x = (-√33-1)/4
(iii) 4x 2 + 4√3x + 3 = 0
समीकरण को 2 +2ab+b 2 रूप में बदलने पर, हम प्राप्त करते हैं,
(2x) 2 + 2 × 2x × √3 + (√3) 2 = 0
(2x + √3) 2 = 0
(2x + 3) = 0 और (2x + √3) = 0
इसलिए, या तो x = -√3/2 या x = -√3/2।
(iv) 2x 2 + x + 4 = 0
2x 2 + x = -4
समीकरण के दोनों पक्षों को 2 से भाग देने पर, हम प्राप्त करते हैं
⇒ एक्स 2 + 1/2x = 2
x 2 + 2 × x × 1/4 = -2
समीकरण के दोनों पक्षों में (1/4) 2 जोड़ने पर, हम प्राप्त करते हैं
(x) 2 + 2 × x × 1/4 + (1/4) 2 = (1/4) 2 - 2
(x + 1/4) 2 = 1/16 - 2
(एक्स + 1/4) 2 = -31/16
जैसा कि हम जानते हैं, संख्याओं का वर्ग ऋणात्मक नहीं हो सकता।
इसलिए, दिए गए समीकरण 2x 2 + x + 4 = 0 का कोई वास्तविक मूल नहीं है ।
2. द्विघात सूत्र को लागू करके ऊपर Q.1 में दिए गए द्विघात समीकरणों के मूल ज्ञात कीजिए।
(i) 2x 2 - 7x + 3 = 0
दिए गए समीकरण की ax 2 + bx + c = 0 से तुलना करने पर, हम प्राप्त करते हैं,
ए = 2, बी = -7 और सी = 3
द्विघात सूत्र का उपयोग करके, हम प्राप्त करते हैं,
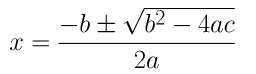
⇒ एक्स = (7±√(49 - 24))/4
⇒ एक्स = (7±√25)/4
⇒ एक्स = (7 ± 5) / 4
⇒ x = (7+5)/4 या x = (7-5)/4
एक्स = 12/4 या 2/4
एक्स = 3 या 1/2
(ii) 2x 2 + x - 4 = 0
दिए गए समीकरण की ax 2 + bx + c = 0 से तुलना करने पर, हम प्राप्त करते हैं,
ए = 2, बी = 1 और सी = -4
द्विघात सूत्र का उपयोग करके, हम प्राप्त करते हैं,
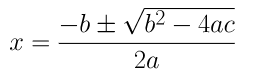
x = (-1±√1+32)/4
x = (-1±√33)/4
∴ x = (-1+√33)/4 या x = (-1-√33)/4
(iii) 4x 2 + 4√3x + 3 = 0
दिए गए समीकरण की कुल्हाड़ी 2 + bx + c = 0 से तुलना करने पर, हम प्राप्त करते हैं
ए = 4, बी = 4√3 और सी = 3
द्विघात सूत्र का उपयोग करके, हम प्राप्त करते हैं,
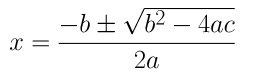
एक्स = (-4√3±√48-48)/8
⇒ एक्स = (-4√3±0)/8
∴ एक्स = -√3/2 या एक्स = -√3/2
(iv) 2x 2 + x + 4 = 0
दिए गए समीकरण की ax 2 + bx + c = 0 से तुलना करने पर, हम प्राप्त करते हैं,
ए = 2, बी = 1 और सी = 4
द्विघात सूत्र का उपयोग करके, हम प्राप्त करते हैं
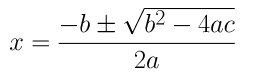
⇒ एक्स = (-1±√1-32)/4
⇒ एक्स = (-1±√-31)/4
जैसा कि हम जानते हैं, किसी संख्या का वर्ग कभी भी ऋणात्मक नहीं हो सकता। अतः दिए गए समीकरण का कोई वास्तविक हल नहीं है।
3. निम्नलिखित समीकरणों के मूल ज्ञात कीजिए:
(i) x-1/x = 3, x 0
(ii) 1/x+4 - 1/x-7 = 11/30, x = -4, 7
समाधान:
(i) x-1/x = 3
एक्स 2 - 3x -1 = 0
दिए गए समीकरण की कुल्हाड़ी 2 + bx + c = 0 से तुलना करने पर, हम प्राप्त करते हैं
ए = 1, बी = -3 और सी = -1
द्विघात सूत्र का उपयोग करके, हम प्राप्त करते हैं,
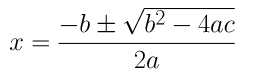
⇒ एक्स = (3±√9+4)/2
⇒ एक्स = (3±√13)/2
∴ x = (3+√13)/2 या x = (3-√13)/2
(ii) 1/x+4 - 1/x-7 = 11/30
x-7-x-4/(x+4)(x-7) = 11/30
-11/(x+4)(x-7) = 11/30
(x+4)(x-7) = -30
x 2 - 3x - 28 = 30
⇒ एक्स 2 - 3x + 2 = 0
हम इस समीकरण को अब गुणनखंडन विधि द्वारा हल कर सकते हैं,
x 2 - 2x - x + 2 = 0
एक्स (एक्स - 2) - 1 (एक्स - 2) = 0
(एक्स - 2) (एक्स - 1) = 0
⇒ एक्स = 1 या 2
4. रहमान की आयु का व्युत्क्रम, (वर्षों में) 3 वर्ष पहले और अब से 5 वर्ष बाद का योग 1/3 है। उसकी वर्तमान आयु ज्ञात कीजिए।
समाधान:
बता दें, रहमान की वर्तमान आयु x वर्ष है।
तीन वर्ष पूर्व रहमान की आयु ( x - 3) वर्ष थी।
पांच वर्ष बाद उसकी आयु ( x + 5) वर्ष होगी।
दिया गया है, 3 साल पहले और 5 साल बाद रहमान की उम्र के व्युत्क्रमों का योग 1/3 के बराबर है।
∴ 1/ x -3 + 1/ x -5 = 1/3
(एक्स +5+ एक्स -3)/( एक्स -3) ( एक्स +5) = 1/3
(2 x +2)/( x -3)( x +5) = 1/3
3(2 x + 2) = ( x -3)( x +5)
6 x + 6 = x 2 + 2 x - 15
एक्स 2 - 4 एक्स - 21 = 0
एक्स 2 - 7 एक्स + 3 एक्स - 21 = 0
एक्स ( एक्स - 7) + 3 ( एक्स - 7) = 0
( एक्स - 7)( एक्स + 3) = 0
एक्स = 7, -3
जैसा कि हम जानते हैं, उम्र नकारात्मक नहीं हो सकती।
अतः रहमान की वर्तमान आयु 7 वर्ष है।
5. एक कक्षा परीक्षण में, शेफाली के गणित और अंग्रेजी में प्राप्तांकों का योग 30 है। यदि उसे गणित में 2 अंक अधिक और अंग्रेजी में 3 अंक कम मिलते, तो उनके अंकों का गुणनफल 210 होता। दोनों में उसके अंक ज्ञात कीजिए। विषय
समाधान:
बता दें, गणित में शेफाली के अंक x हैं।
फिर, अंग्रेजी में अंक 30 - x होंगे।
दिए गए प्रश्न के अनुसार,
(एक्स + 2)(30 - एक्स - 3) = 210
(एक्स + 2) (27 - एक्स) = 210
-x 2 + 25x + 54 = 210
⇒ एक्स 2 - 25x + 156 = 0
⇒ x 2 - 12x - 13x + 156 = 0
एक्स (एक्स - 12) -13 (एक्स - 12) = 0
(एक्स - 12) (एक्स - 13) = 0
एक्स = 12, 13
इसलिए, यदि गणित में अंक 12 हैं, तो अंग्रेजी में अंक 30 - 12 = 18 होंगे और गणित में अंक 13 होंगे, तो अंग्रेजी में अंक 30 - 13 = 17 होंगे ।
6. एक आयताकार मैदान का विकर्ण छोटी भुजा से 60 मीटर अधिक है। यदि लंबी भुजा छोटी भुजा से 30 मीटर अधिक है, तो मैदान की भुजाएँ ज्ञात कीजिए।
समाधान:
मान लीजिए, आयत की छोटी भुजा x m है।
तब, आयत की बड़ी भुजा = ( x + 30) m
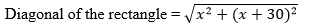
जैसा दिया गया है, विकर्ण की लंबाई = x + 30 m . है
इसलिए,
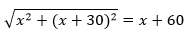
एक्स 2 + ( एक्स + 30) 2 = ( एक्स + 60) 2
⇒ x 2 + x 2 + 900 + 60 x = x 2 + 3600 + 120 x
x 2 - 60 x - 2700 = 0
x 2 - 90 x + 30 x - 2700 = 0
एक्स ( एक्स - 90) + 30 ( एक्स -90 ) = 0
( एक्स - 90)( एक्स + 30) = 0
एक्स = 90, -30
हालाँकि, क्षेत्र का पक्ष ऋणात्मक नहीं हो सकता। अतः छोटी भुजा की लंबाई 90 मीटर होगी।
और बड़ी भुजा की लंबाई (90 + 30) m = 120 m होगी।
7. दो संख्याओं के वर्गों का अंतर 180 है। छोटी संख्या का वर्ग बड़ी संख्या का 8 गुना है। दो नंबर खोजें।
समाधान:
मान लीजिए, बड़ी और छोटी संख्या क्रमशः x और y है।
दिए गए प्रश्न के अनुसार,
x 2 - y 2 = 180 और y 2 = 8 x
एक्स 2 - 8 एक्स = 180
x 2 - 8 x - 180 = 0
x 2 - 18 x + 10 x - 180 = 0
एक्स ( एक्स - 18) +10 ( एक्स - 18) = 0
( एक्स - 18)( एक्स + 10) = 0
एक्स = 18, -10
हालाँकि, बड़ी संख्या को ऋणात्मक संख्या नहीं माना जा सकता है, क्योंकि बड़ी संख्या का 8 गुना ऋणात्मक होगा और इसलिए, छोटी संख्या का वर्ग ऋणात्मक होगा जो संभव नहीं है।
अतः बड़ी संख्या केवल 18 होगी।
एक्स = 18
y 2 = 8x = 8 × 18 = 144
y = ±√144 = ± 12
छोटी संख्या = ±12
इसलिए, संख्याएँ 18 और 12 या 18 और -12 हैं।
8. एक ट्रेन एकसमान चाल से 360 किमी की यात्रा करती है। यदि गति 5 किमी/घंटा अधिक होती, तो वह उसी यात्रा में 1 घंटा कम समय लेती। ट्रेन की गति पाएं।
समाधान:
मान लीजिए, ट्रेन की गति x किमी/घंटा है।
360 किमी की दूरी तय करने में लगा समय = 360/ x घंटा।
दिए गए प्रश्न के अनुसार,
( x + 5)(360/x – 1) = 360
360 - x + 1800/x-5 = 360
एक्स 2 + 5 एक्स - 1800 = 0
x 2 + 45x - 40x - 1800 = 0
एक्स ( एक्स + 45) -40 ( एक्स + 45) = 0
( x + 45)( x – 40) = 0
एक्स = 40, -45
जैसा कि हम जानते हैं, गति का मान ऋणात्मक नहीं हो सकता।
अत: ट्रेन की गति 40 किमी/घंटा है।
9. दो पानी के नल एक साथ एक टैंक को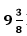
घंटों में भर सकते हैं। बड़े व्यास वाले नल को टैंक को अलग से भरने में छोटे वाले से 10 घंटे कम लगते हैं। वह समय ज्ञात कीजिए जिसमें प्रत्येक नल अलग से टंकी को भर सकता है।
समाधान:
माना छोटे पाइप द्वारा टंकी को भरने में लिया गया समय = x घंटा।
बड़े पाइप द्वारा लिया गया समय = ( x - 10) घंटा
छोटे पाइप द्वारा 1 घंटे में भरा गया टैंक का भाग = 1/ x
बड़े पाइप द्वारा 1 घंटे में भरा गया टैंक का भाग = 1/( x - 10)
जैसा दिया गया है, टैंक को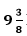
दोनों पाइपों द्वारा मिलाकर = 75/8 घंटे में भरा जा सकता है।
इसलिए,
1/ x + 1/ x -10 = 8/75
एक्स -10+ एक्स / एक्स ( एक्स -10) = 8/75
2 x -10/ x ( x -10) = 8/75
75(2 x - 10) = 8 x 2 - 80 x
⇒ 150 x - 750 = 8 x 2 - 80 x
8 x 2 - 230 x +750 = 0
8 x 2 - 200 x - 30 x + 750 = 0
8 एक्स ( एक्स - 25) -30 ( एक्स - 25) = 0
( x - 25)(8 x -30) = 0
एक्स = 25, 30/8
छोटे पाइप द्वारा लिया गया समय 30/8 = 3.75 घंटे नहीं हो सकता, क्योंकि बड़े पाइप द्वारा लिया गया समय ऋणात्मक हो जाएगा, जो तार्किक रूप से संभव नहीं है।
इसलिए, छोटे पाइप और बड़े पाइप द्वारा अलग-अलग लिया गया समय क्रमशः 25 और 25 - 10 =15 घंटे होगा।
10. मैसूर और बैंगलोर के बीच 132 किमी की यात्रा करने के लिए एक एक्सप्रेस ट्रेन एक यात्री ट्रेन से 1 घंटे कम समय लेती है (बिना इंटरमीडिएट स्टेशनों पर रुकने के समय को ध्यान में रखे)। यदि एक्सप्रेस ट्रेन की औसत गति यात्री ट्रेन की औसत गति से 11 किमी/घंटा अधिक है, तो दोनों ट्रेनों की औसत गति ज्ञात कीजिए।
समाधान:
मान लीजिए, यात्री ट्रेन की औसत गति = x किमी/घंटा।
एक्सप्रेस ट्रेन की औसत गति = ( x + 11) किमी/घंटा
दिया गया है, एक्सप्रेस ट्रेन द्वारा 132 किमी की दूरी तय करने में लगने वाला समय समान दूरी को कवर करने के लिए यात्री ट्रेन से 1 घंटे कम है। इसलिए,
(132/x) - (132/(x+11)) = 1
132(x+11-x)/(x(x+11)) = 1
132 × 11 /(x(x+11)) = 1
132 × 11 = x ( x + 11)
एक्स 2 + 11 एक्स - 1452 = 0
एक्स 2 + 44 एक्स -33 एक्स -1452 = 0
एक्स ( एक्स + 44) -33 ( एक्स + 44) = 0
( x + 44)( x – 33) = 0
एक्स = - 44, 33
जैसा कि हम जानते हैं, गति ऋणात्मक नहीं हो सकती।
अतः पैसेंजर ट्रेन की गति 33 किमी/घंटा होगी और इस प्रकार एक्सप्रेस ट्रेन की गति 33 + 11 = 44 किमी/घंटा होगी।
11. दो वर्गों के क्षेत्रफल का योग 468 मीटर 2 है । यदि उनके परिमापों का अंतर 24 मी है, तो दोनों वर्गों की भुजाएँ ज्ञात कीजिए।
समाधान:
माना कि दो वर्गों की भुजाएँ x m और y m हैं।
अत: उनका परिमाप क्रमशः 4 x और 4 y होगा
और वर्गों का क्षेत्रफल क्रमशः x 2 और y 2 होगा।
दिया गया,
4 x - 4 y = 24
एक्स - वाई = 6
एक्स = वाई + 6
साथ ही, x 2 + y 2 = 468
(6 + y 2 ) + y 2 = 468
36 + y 2 + 12 y + y 2 = 468
2 y 2 + 12 y + 432 = 0
y 2 + 6y - 216 = 0
y 2 + 18 y - 12 y - 216 = 0
वाई ( वाई +18) -12( वाई + 18) = 0
( y + 18)( y – 12) = 0
वाई = -18, 12
जैसा कि हम जानते हैं, वर्ग की भुजा ऋणात्मक नहीं हो सकती।
अतः, वर्गों की भुजाएँ 12 m और (12 + 6) m = 18 m हैं।
Exercise - 4.4 पृष्ठ: 91
1. निम्नलिखित द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। अगर असली जड़ें मौजूद हैं, तो उन्हें खोजें;
(i) 2 x 2 - 3 x + 5 = 0
(ii) 3 x 2 - 4√3 x + 4 = 0
(iii) 2 x 2 - 6 x + 3 = 0
समाधान:
(मैंने दे दिया,
2x 2 - 3 x + 5 = 0
कुल्हाड़ी 2 + बीएक्स + सी = 0 के साथ समीकरण की तुलना करने पर , हम प्राप्त करते हैं
ए = 2, बी = -3 और सी = 5
हम जानते हैं, विभेदक = b 2 - 4 ac
= ( - 3) 2 - 4 (2) (5) = 9 - 40
= - 31
जैसा कि आप देख सकते हैं, बी 2 - 4ac <0
इसलिए, दिए गए समीकरण 2x 2 - 3 x + 5 = 0 के लिए कोई वास्तविक मूल संभव नहीं है।
(ii) 3 x 2 - 4√3 x + 4 = 0
कुल्हाड़ी 2 + बीएक्स + सी = 0 के साथ समीकरण की तुलना करने पर , हम प्राप्त करते हैं
ए = 3, बी = -4√3 और सी = 4
हम जानते हैं, विभेदक = b 2 - 4 ac
= (-4√3) 2 - 4(3)(4)
= 48 - 48 = 0
बी 2 - 4 एसी = 0 के रूप में,
दिए गए समीकरण के वास्तविक मूल मौजूद हैं और वे एक दूसरे के बराबर हैं।
अत: मूल होंगे – b /2 a और – b /2 a ।
- b /2 a = -(-4√3)/2×3 = 4√3/6 = 2√3/3 = 2/√3
इसलिए, मूल 2/√3 और 2/√3 हैं।
(iii) 2 x 2 - 6 x + 3 = 0
कुल्हाड़ी 2 + बीएक्स + सी = 0 के साथ समीकरण की तुलना करने पर , हम प्राप्त करते हैं
ए = 2, बी = -6, सी = 3
जैसा कि हम जानते हैं, विभेदक = b 2 - 4 ac
= (-6) 2 - 4 (2) (3)
= 36 - 24 = 12
बी 2 - 4 एसी > 0 के रूप में,
इसलिए, इस समीकरण के लिए अलग-अलग वास्तविक मूल मौजूद हैं, 2 x 2 - 6 x + 3 = 0।
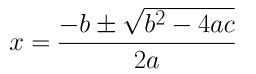
= (-(-6) ± (-6 2 -4(2)(3)) )/2(2)
= (6 ± 2√3 ) / 4
= (3±√3)/2
इसलिए दिए गए समीकरण के मूल हैं (3+√3)/2 तथा (3-√3)/2
2. निम्नलिखित द्विघात समीकरणों में से प्रत्येक के लिए k के मान ज्ञात कीजिए, ताकि उनके दो बराबर मूल हों।
(i) 2 x 2 + kx + 3 = 0
(ii) kx ( x - 2) + 6 = 0
समाधान:
(i) 2 x 2 + kx + 3 = 0
दिए गए समीकरण की ax 2 + bx + c = 0 से तुलना करने पर, हम प्राप्त करते हैं,
ए = 2, बी = के और सी = 3
जैसा कि हम जानते हैं, विभेदक = b 2 - 4 ac
= ( के ) 2 - 4(2) (3)
= कश्मीर 2 - 24
समान जड़ों के लिए, हम जानते हैं,
विभेदक = 0
कश्मीर 2 - 24 = 0
कश्मीर 2 = 24
के = ±√24 = ±2√6
(ii) केएक्स ( एक्स - 2) + 6 = 0
या केएक्स 2 - 2 केएक्स + 6 = 0
दिए गए समीकरण की ax 2 + bx + c = 0 से तुलना करने पर हमें प्राप्त होता है
ए = के , बी = - 2 के और सी = 6
हम जानते हैं, विभेदक = b 2 - 4 ac
= (-2 के ) 2 - 4 ( के ) (6)
= 4 के 2 - 24 के
समान जड़ों के लिए, हम जानते हैं,
बी 2 - 4 एसी = 0
4 के 2 - 24 के = 0
4 के ( के - 6) = 0
या तो 4 k = 0 या k = 6 = 0
के = 0 या के = 6
हालाँकि, यदि k = 0 है, तो समीकरण में ' x 2 ' और ' x ' पद नहीं होंगे।
इसलिए, यदि इस समीकरण के दो बराबर मूल हैं, तो k केवल 6 होना चाहिए।
3. क्या एक आयताकार आम का बाग बनाना संभव है जिसकी लंबाई उसकी चौड़ाई से दोगुनी हो और क्षेत्रफल 800 मीटर 2 हो? यदि हां, तो इसकी लंबाई और चौड़ाई ज्ञात कीजिए।
समाधान:
मान लीजिए मैंगो ग्रोव की चौड़ाई l है ।
मैंगो ग्रोव की लंबाई 2 लीटर होगी ।
मैंगो ग्रोव का क्षेत्रफल = (2 l ) ( l )= 2 l 2
2 एल 2 = 800
एल 2 = 800/2 = 400
एल 2 - 400 = 0
दिए गए समीकरण की ax 2 + bx + c = 0 से तुलना करने पर हमें प्राप्त होता है
ए = 1, बी = 0, सी = 400
जैसा कि हम जानते हैं, विभेदक = b 2 - 4 ac
=> (0) 2 - 4 × (1) × (- 400) = 1600
यहां, बी 2 - 4 एसी > 0
इस प्रकार, समीकरण के वास्तविक मूल होंगे। और इसलिए, वांछित आयताकार आम के ग्रोव को डिजाइन किया जा सकता है।
एल = ± 20
जैसा कि हम जानते हैं, लंबाई का मान ऋणात्मक नहीं हो सकता।
अत: आम के बाग की चौड़ाई = 20 m
मैंगो ग्रोव की लंबाई = 2 × 20 = 40 मी
4. क्या निम्नलिखित स्थिति संभव है? यदि हां, तो उनकी वर्तमान आयु ज्ञात कीजिए। दो मित्रों की आयु का योग 20 वर्ष है। चार वर्ष पहले, उनकी आयु का वर्षों में गुणनफल 48 था।
समाधान:
मान लीजिए, एक मित्र की आयु x वर्ष है।
फिर, दूसरे मित्र की आयु (20 - x) वर्ष होगी।
चार साल पूर्व,
पहले मित्र की आयु = ( x - 4) वर्ष
दूसरे मित्र की आयु = (20 - x - 4) = (16 - x ) वर्ष
दिए गए प्रश्न के अनुसार हम लिख सकते हैं,
( एक्स - 4) (16 - एक्स ) = 48
16 x - x 2 - 64 + 4 x = 48
- x 2 + 20 x - 112 = 0
एक्स 2 - 20 एक्स + 112 = 0
कुल्हाड़ी 2 + बीएक्स + सी = 0 के साथ समीकरण की तुलना करने पर , हम प्राप्त करते हैं
ए = 1 , बी = -2 0 और सी = 112
विभेदक = ख 2 - 4 ac
= (- 20 ) 2 - 4 × 112
= 400 - 448 = -48
बी 2 - 4 एसी <0
इसलिए, समीकरणों के लिए कोई वास्तविक समाधान संभव नहीं होगा। इसलिए, स्थिति मौजूद नहीं है।
5. क्या परिमाप 80 और क्षेत्रफल 400 मी का एक आयताकार पार्क बनाना संभव है? यदि ऐसा है तो इसकी लंबाई और चौड़ाई पाएं।
समाधान:
माना पार्क की लंबाई और चौड़ाई l और b है।
आयताकार पार्क का परिमाप = 2 ( l + b ) = 80
तो, एल + बी = 40
या, बी = 40 - एल
आयताकार पार्क का क्षेत्रफल = l×b = l(40 – l) = 40 l – l 2 = 400
l 2 - 40 l + 400 = 0, जो एक द्विघात समीकरण है।
कुल्हाड़ी 2 + बीएक्स + सी = 0 के साथ समीकरण की तुलना करने पर , हम प्राप्त करते हैं
ए = 1, बी = -40, सी = 400
चूँकि, विभेदक = b 2 - 4 ac
=(- 40 ) 2 - 4 × 400
= 1600 - 1600 = 0
अत: b 2 - 4 ac = 0
इसलिए, इस समीकरण के वास्तविक मूल समान हैं। इसलिए स्थिति संभव है।
समीकरण की जड़,
एल = - बी / 2 ए
एल = -(-40)/2(1) = 40/2 = 20
अत: आयताकार पार्क की लंबाई, l = 20 m
और पार्क की चौड़ाई, b = 40 - l = 40 - 20 = 20 m।
