एनसीईआरटी सॉल्यूशंस फॉर क्लास 10 मैथ्स चैप्टर 11 रचनाएँ विस्तृत तरीके से प्रदान किए गए हैं, जहां कोई भी तेजी से संशोधन के लिए सभी प्रश्नों का चरण-दर-चरण समाधान ढूंढ सकता है। एनसीईआरटी कक्षा 10 के गणित के 11 वें अध्याय के समाधान एनसीईआरटी के दिशानिर्देशों के तहत विषय विशेषज्ञों द्वारा छात्रों को उनकी दूसरी अवधि की परीक्षा की तैयारी में सहायता करने के लिए तैयार किए जाते हैं। दूसरे सत्र की परीक्षा की तैयारी में तेजी लाने के लिए itselfu पर कक्षा 10 गणित, अध्याय 11 - निर्माण के लिए मुफ्त एनसीईआरटी समाधान प्राप्त करें। एनसीईआरटी अभ्यास के सभी प्रश्नों को निर्माण के लिए चरण-दर-चरण प्रक्रिया के साथ आरेखों का उपयोग करके हल किया जाता है। एनसीईआरटी के समाधान छात्रों को उनकी अवधारणाओं को बढ़ावा देने और शंकाओं को दूर करने में मदद करते हैं।
गणित एनसीईआरटी अध्याय 11 के उत्तर एक्सेस करें - रचनाएँ
Exercise 11.1 पृष्ठ: 220
निम्नलिखित में से प्रत्येक में, निर्माण का औचित्य भी दीजिए:
1. 7.6 सेमी लंबा एक रेखाखंड खींचिए और इसे 5:8 के अनुपात में विभाजित कीजिए। दोनों भागों को मापिए ।
समाधान :
7.6 सेमी लंबाई वाले एक रेखा खंड को 5:8 के अनुपात में निम्नानुसार विभाजित किया गया है।
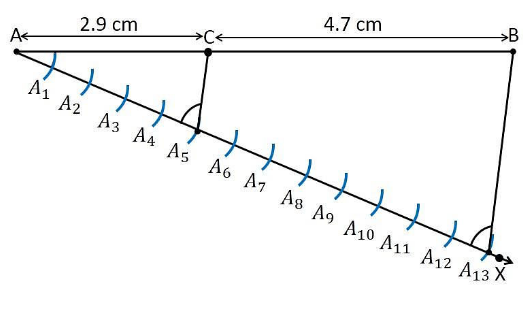
1. 7.6 सेमी . की लंबाई का रेखाखंड AB खींचिए
2. एक किरण AX खींचिए जो रेखाखंड AB से न्यून कोण बनाती है।
3. किरण AX पर बिंदुओं अर्थात, 13 (= 5+8) बिंदुओं, जैसे A1, A2, A3, A4 …….. A13 को इस प्रकार खोजें कि यह AA1 = A1A2 = A2A3 इत्यादि बन जाए।
4. रेखाखंड और किरण, BA13 को मिलाइए।
5. बिंदु A5 से होकर BA13 के समांतर एक रेखा खींचिए जो AA13B . के बराबर कोण बनाती है
6. बिंदु A5 जो रेखा AB को बिंदु C पर प्रतिच्छेद करता है।
7. C, 7.6 सेमी के रेखाखंड AB को 5:8 के आवश्यक अनुपात में विभाजित करने वाला बिंदु है।
8. अब, रेखा AC और CB की लंबाई मापें। यह क्रमशः 2.9 सेमी और 4.7 सेमी के माप के लिए निकलता है।
औचित्य:
दी गई समस्या के निर्माण को सिद्ध करके उचित ठहराया जा सकता है
एसी/सीबी = 5/8
निर्माण से, हमारे पास A5C है || ए13बी. त्रिभुज AA13B के लिए मूल आनुपातिकता प्रमेय से, हम प्राप्त करते हैं
एसी/सीबी = एए 5 /ए 5 ए 13 ..... (1)
निर्मित आकृति से, यह देखा गया है कि AA5 और A5A13 में रेखाखंडों के क्रमशः 5 और 8 समान विभाजन हैं।
इसलिए, यह बन जाता है
एए 5 /ए 5 ए 13 =5/8… (2)
समीकरणों (1) और (2) की तुलना करें, हम प्राप्त करते हैं
एसी/सीबी = 5/8
अत: न्यायोचित है।
2. 4 सेमी, 5 सेमी और 6 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर उसके समरूप एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ 2/3 हैं।
पहले त्रिभुज की संगत भुजाएँ।
समाधान :
1. एक रेखाखंड AB खींचिए जिसका माप 4 सेमी, अर्थात AB = 4 सेमी है।
2. बिंदु A को केंद्र मानकर 5 cm त्रिज्या का एक चाप खींचिए।
3. इसी प्रकार, बिंदु B को उसका केंद्र मानकर 6 सेमी त्रिज्या का एक चाप खींचिए।
4. खींचे गए चाप एक दूसरे को बिंदु C पर काटेंगे।
5. अब, हमने AC = 5 सेमी और BC = 6 सेमी प्राप्त किया है और इसलिए ABC अभीष्ट त्रिभुज है।
6. एक किरण AX खींचिए जो शीर्ष C के विपरीत दिशा में रेखाखंड AB से न्यून कोण बनाती है।
7. लाइन AX पर 3 बिंदु जैसे A1, A2, A3 (जैसा कि 3 2 और 3 के बीच बड़ा है) का पता लगाएँ जैसे कि यह AA1 = A1A2 = A2A3 हो जाए।
8. बिंदु BA3 को मिलाइए और A2 से होकर एक रेखा खींचिए जो रेखा BA3 के समानांतर है जो AB को बिंदु B' पर काटती है।
9. बिंदु B' से होकर रेखा BC के समांतर एक रेखा खींचिए जो रेखा AC को C' पर प्रतिच्छेद करती है।
10. इसलिए, AB'C' अभीष्ट त्रिभुज है।
औचित्य:
दी गई समस्या के निर्माण को सिद्ध करके उचित ठहराया जा सकता है
एबी '= (2/3) एबी
बी'सी' = (2/3)बीसी
एसी '= (2/3) एसी
रचना से हमें B'C' प्राप्त होता है || ईसा पूर्व
AB'C' = ABC (समान कोण)
AB’C’ और ABC में,
ABC = AB’C (ऊपर सिद्ध)
BAC = B'AC' (सामान्य)
AB’C’ ABC (AA समानता मानदंड से)
इसलिए, AB'/AB = B'C'/BC= AC'/AC…. (1)
AAB’ और AAB में,
A 2 AB' =∠A 3 AB (उभयनिष्ठ)
संगत कोणों से, हम प्राप्त करते हैं,
AA 2 B' =∠AA 3 B
इसलिए, AA समानता मानदंड से, हम प्राप्त करते हैं
एए 2 बी' और एए 3 बी
अतः, AB'/AB = AA 2 /AA 3
इसलिए, AB'/AB = 2/3 ……. (2)
समीकरण (1) और (2) से, हम प्राप्त करते हैं
एबी '/ एबी = बी'सी' / बीसी = एसी '/ एसी = 2/3
इसे इस प्रकार लिखा जा सकता है
एबी '= (2/3) एबी
बी'सी' = (2/3)बीसी
एसी '= (2/3) एसी
इसलिए जायज है।
3. एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ 5 सेमी, 6 सेमी और 7 सेमी हों और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ पहले त्रिभुज की संगत भुजाओं की 7/5 हों।
समाधान :
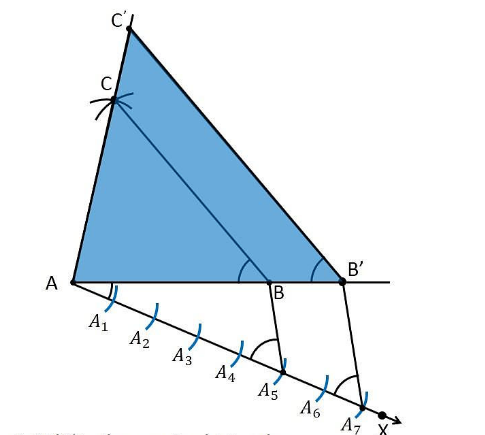
1. एक रेखाखंड AB = 5 सेमी खींचिए।
2. A और B को केंद्र मानकर त्रिज्या 6 सेमी और 7 सेमी के चाप खींचिए।
3. ये चाप एक दूसरे को बिंदु C पर काटेंगे और इसलिए ABC अभीष्ट त्रिभुज है जिसकी भुजाओं की लंबाई क्रमशः 5 सेमी, 6 सेमी और 7 सेमी है।
4. एक किरण AX खींचिए जो शीर्ष C के विपरीत दिशा में रेखाखंड AB से न्यून कोण बनाती है।
5. ए 1 , ए 2 , ए 3 , ए 4 , ए 5 , ए 6 , ए 7 (जैसा कि 7 5 और 7 के बीच बड़ा है) जैसे 7 बिंदुओं को लाइन एएक्स पर इस तरह खोजें कि यह एए 1 = ए बन जाए 1 ए 2 = ए 2 ए 3 = ए 3 ए 4 = ए 4 ए 5 = ए 5 ए 6 = ए 6 ए 7
6. बिंदुओं BA 5 को मिलाइए और A 7 से BA 5 तक एक रेखा खींचिए जो रेखा BA 5 के समानांतर है, जहां यह विस्तारित रेखा खंड AB को बिंदु B' पर काटती है।
7. अब, B' विस्तारित रेखा खंड AC से C' पर एक रेखा खींचिए जो रेखा BC के समानांतर है और यह एक त्रिभुज बनाने के लिए प्रतिच्छेद करती है।
8. इसलिए, AB'C' अभीष्ट त्रिभुज है।
औचित्य:
दी गई समस्या के निर्माण को सिद्ध करके उचित ठहराया जा सकता है
एबी '= (7/5) एबी
बी'सी' = (7/5)बीसी
एसी '= (7/5) एसी
रचना से हमें B'C' प्राप्त होता है || ईसा पूर्व
AB'C' = ABC (समान कोण)
AB’C’ और ABC में,
ABC = AB’C (ऊपर सिद्ध)
BAC = B'AC' (सामान्य)
AB’C’ ABC (AA समानता मानदंड से)
इसलिए, AB'/AB = B'C'/BC= AC'/AC…. (1)
AA 7 B' और AA 5 B में,
A 7 AB'=∠A 5 AB (उभयनिष्ठ)
संगत कोणों से, हम प्राप्त करते हैं,
AA 7 B'=∠AA 5 B
इसलिए, AA समानता मानदंड से, हम प्राप्त करते हैं
ए ए 2 बी' और एए 3 बी
अतः, AB'/AB = AA 5 /AA 7
इसलिए, AB/AB' = 5/7 ……. (2)
समीकरण (1) और (2) से, हम प्राप्त करते हैं
एबी '/ एबी = बी'सी' / बीसी = एसी '/ एसी = 7/5
इसे इस प्रकार लिखा जा सकता है
एबी '= (7/5) एबी
बी'सी' = (7/5)बीसी
एसी '= (7/5) एसी
इसलिए जायज है।
समाधान:
1. 8 सेमी माप का एक रेखाखंड BC खींचिए।
2. अब रेखाखंड BC का लम्ब समद्विभाजक खींचिए और बिंदु D पर प्रतिच्छेद कीजिए
3. बिंदु D को केंद्र के रूप में लें और 4 सेमी की त्रिज्या के साथ एक चाप खींचें जो बिंदु A पर लंबवत समद्विभाजक को काटता है।
4. अब रेखा AB और AC को मिलाइए और त्रिभुज अभीष्ट त्रिभुज है।
5. एक किरण BX खींचिए जो शीर्ष A के विपरीत दिशा में BC रेखा से न्यून कोण बनाती है।
6. किरण BX पर 3 बिंदु B 1 , B 2 और B 3 इस प्रकार लगाएं कि BB 1 = B 1 B 2 = B 2 B 3
7. बिंदु B 2 C को मिलाइए और B 3 से एक रेखा खींचिए जो रेखा B 2 C के समानांतर है, जहां यह विस्तारित रेखा खंड BC को बिंदु C' पर काटती है।
8. अब, C' विस्तारित रेखा खंड AC से A' पर एक रेखा खींचिए जो रेखा AC के समानांतर है और यह एक त्रिभुज बनाने के लिए प्रतिच्छेद करती है।
9. इसलिए, A'BC' अभीष्ट त्रिभुज है।
औचित्य:
दी गई समस्या के निर्माण को सिद्ध करके उचित ठहराया जा सकता है
ए'बी = (3/2) एबी
बीसी' = (3/2)बीसी
एसी '= (3/2) एसी
रचना से हमें A'C' प्राप्त होता है || एसी
A'C'B = ACB (समान कोण)
A'BC' और ABC में,
B = B (सामान्य)
A'BC' = ACB
A'BC' ABC (AA समानता मानदंड से)
इसलिए, ए'बी/एबी = बीसी'/बीसी = ए'सी'/एसी
चूँकि समरूप त्रिभुज की संगत भुजाएँ समान अनुपात में होती हैं, यह बन जाती है
ए'बी/एबी = बीसी'/बीसी = ए'सी'/एसी = 3/2
इसलिए जायज है।
5. एक त्रिभुज ABC खींचिए जिसकी भुजा BC = 6 सेमी, AB = 5 सेमी और ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की 3/4 हों।
समाधान:
निर्माण करना: BC = 6 सेमी, AB = 5 सेमी और 
ABC = भुजा वाले एक त्रिभुज ABC की रचना करना 
और फिर उसके समरूप एक त्रिभुज की रचना करना जिसकी भुजाएँ 
पहले त्रिभुज ABC की संगत भुजाओं की हों।
निर्माण के चरण:
(a) एक त्रिभुज ABC खींचिए जिसकी भुजा BC = 6 सेमी, AB = 5 सेमी और ABC = हो ।
(बी) बिंदु बी से, एक किरण बीएक्स खींचें, जो बीसी के साथ शीर्ष ए के विपरीत दिशा में एक न्यून कोण बनाती है।
(सी) बीएक्स पर 4 बिंदुओं का पता लगाएं 
जैसे कि 
।
(डी) 
बिंदु के माध्यम से एक रेखा खींचें और बीसी को बिंदु सी पर काटने 
के समानांतर एक रेखा खींचें । (ई) सी' के माध्यम से रेखा सीए के समानांतर एक रेखा खींचें जो बीए को ए पर काटती है।
तब, ABC' अभीष्ट त्रिभुज है।
औचित्य:
परंतु 
इसलिए, 
………(i)
सीए 
सी'ए'
बीसीए ' 
बीसीए '
अत: हमें दिए गए त्रिभुज के समरूप नया त्रिभुज प्राप्त होता है, जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की 34 34 वीं के बराबर होती हैं।
6. एक त्रिभुज ABC खींचिए जिसकी भुजा BC = 7 सेमी, B = 45°, A = 105° हो। फिर, एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ ABC की संगत भुजाओं की 4/3 गुनी हों।
C खोजने के लिए:
दिया गया:
B = 45°, A = 105°
हम जानते हैं कि,
त्रिभुज के सभी अंतः कोणों का योग 180° होता है।
A+∠B +∠C = 180°
105°+45°+∠C = 180°
∠C = 180° - 150°
C = 30°
अत: त्रिभुज के गुणधर्म से हमें ∠C = 30° . प्राप्त होता है
समाधान:
वांछित त्रिभुज को निम्नानुसार खींचा जा सकता है।
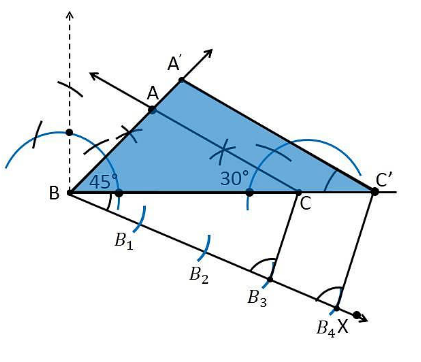
1. आधार BC = 7 सेमी, ∠B = 45° और C = 30° के पार्श्व मापों के साथ एक ABC खींचिए।
2. एक किरण खींचिए जो BX शीर्ष A के विपरीत दिशा में BC से न्यून कोण बनाती है।
3. किरण BX पर 4 बिन्दुओं का पता लगाएँ (क्योंकि 4 और 3 में 4 बड़ा है), जैसे B1, B2, B3, B4,।
4. बिंदुओं B3C को मिलाइए।
5. B4 से होकर B3C के समांतर एक रेखा खींचिए जो विस्तारित रेखा BC को C' पर प्रतिच्छेद करती है।
6. C' से होकर रेखा AC के समांतर एक रेखा खींचिए जो विस्तारित रेखाखंड को C' पर प्रतिच्छेद करती है।
7. इसलिए, A'BC' अभीष्ट त्रिभुज है।
औचित्य:
दी गई समस्या के निर्माण को सिद्ध करके उचित ठहराया जा सकता है
चूंकि स्केल फैक्टर 4/3 है, इसलिए हमें साबित करना होगा
ए'बी = (4/3) एबी
बीसी' = (4/3)बीसी
एसी '= (4/3) एसी
रचना से हमें A'C' प्राप्त होता है || एसी
A'BC' और ABC में,
A'C'B = ACB (समान कोण)
B = B (सामान्य)
A'BC' ABC (AA समानता मानदंड से)
चूँकि समरूप त्रिभुज की संगत भुजाएँ समान अनुपात में होती हैं, यह बन जाती है
इसलिए, ए'बी/एबी = बीसी'/बीसी = ए'सी'/एसी
तो, यह बन जाता है A'B/AB = BC'/BC= A'C'/AC = 4/3
इसलिए जायज है।
7. एक समकोण त्रिभुज खींचिए जिसकी भुजाएँ (कर्ण को छोड़कर) 4 सेमी और 3 सेमी लंबी हों। फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए गए त्रिभुज की संगत भुजाओं की 5/3 गुनी हों।
दिया गया:
कर्ण के अलावा अन्य भुजाओं की लंबाई 4cm और 3cm है। यह परिभाषित करता है कि पक्ष एक दूसरे के लंबवत हैं
समाधान:
वांछित त्रिभुज को निम्नानुसार खींचा जा सकता है।
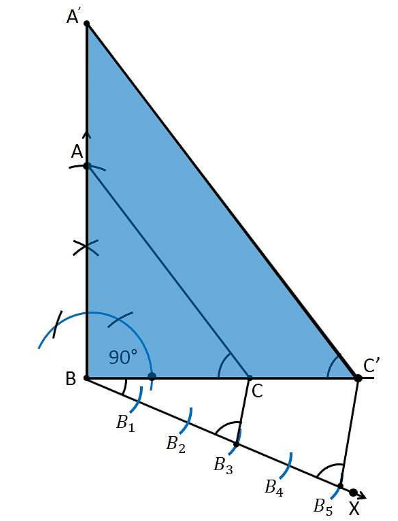
1. एक रेखाखंड BC =3 cm खींचिए।
2. अब 90° का कोण मापें और खींचे
3. B को केंद्र मानकर 4 cm त्रिज्या वाला एक चाप खींचिए और किरण को बिंदु B पर काटता है।
4. अब, रेखाओं AC को मिलाइए और त्रिभुज ABC अभीष्ट त्रिभुज है।
5. एक किरण खींचिए जो BX शीर्ष A के विपरीत दिशा में BC से न्यून कोण बनाती है।
6. किरण BX पर 5 जैसे B1, B2, B3, B4, इस प्रकार लगाएं कि BB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B 5
7. बिंदुओं B3C को मिलाइए।
8. B5 से होकर B3C के समांतर एक रेखा खींचिए जो विस्तारित रेखा BC को C' पर प्रतिच्छेद करती है।
9. C' से होकर रेखा AC के समांतर एक रेखा खींचिए जो विस्तारित रेखा AB को A' पर प्रतिच्छेद करती है।
10. इसलिए, A'BC' अभीष्ट त्रिभुज है।
औचित्य:
दी गई समस्या के निर्माण को सिद्ध करके उचित ठहराया जा सकता है
चूंकि स्केल फैक्टर 5/3 है, इसलिए हमें साबित करना होगा
ए'बी = (5/3) एबी
बीसी' = (5/3)बीसी
एसी '= (5/3) एसी
रचना से हमें A'C' प्राप्त होता है || एसी
A'BC' और ABC में,
A'C'B = ACB (समान कोण)
B = B (सामान्य)
A'BC' ABC (AA समानता मानदंड से)
चूँकि समरूप त्रिभुज की संगत भुजाएँ समान अनुपात में होती हैं, यह बन जाती है
इसलिए, ए'बी/एबी = बीसी'/बीसी = ए'सी'/एसी
तो, यह बन जाता है A'B/AB = BC'/BC= A'C'/AC = 5/3
इसलिए जायज है।
Exercise - 11.2 पृष्ठ: 221
निम्नलिखित में से प्रत्येक में, निर्माण का औचित्य भी दीजिए:
1. त्रिज्या 6 सेमी का एक वृत्त खींचिए। इसके केंद्र से 10 सेमी दूर एक बिंदु से वृत्त पर स्पर्श रेखाओं का युग्म बनाइए और उनकी लंबाई मापिए।
समाधान:
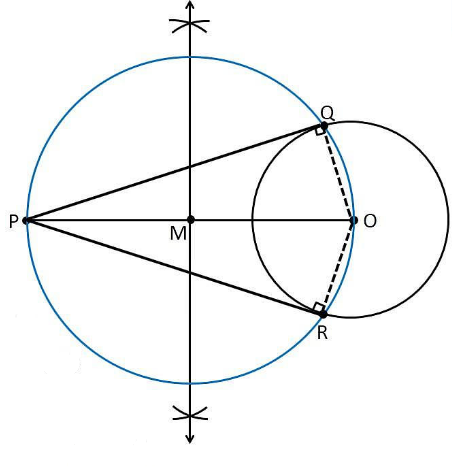
दिए गए वृत्त पर स्पर्श रेखाओं का एक युग्म खींचने की रचना इस प्रकार है।
1. त्रिज्या = 6 सेमी, जिसका केंद्र 0 है, वाला एक वृत्त खींचिए।
2. एक बिंदु P ज्ञात कीजिए, जो O से 10 सेमी की दूरी पर है।
3. बिंदुओं O और P को रेखा से मिलाइए
4. रेखा OP का लम्ब समद्विभाजक खींचिए।
5. मान लीजिए M रेखा PO का मध्य-बिंदु है।
6. M को केंद्र मानकर MO . की लंबाई मापिए
7. लंबाई MO को त्रिज्या के रूप में लिया जाता है और एक वृत्त खींचा जाता है।
8. MO की त्रिज्या से खींचा गया वृत्त पिछले वृत्त को बिंदु Q और R पर प्रतिच्छेद करता है।
9. PQ और PR को मिलाइए।
10. इसलिए, PQ और PR अभीष्ट स्पर्श रेखाएँ हैं।
औचित्य:
दी गई समस्या की रचना को यह सिद्ध करके न्यायोचित ठहराया जा सकता है कि PQ और PR, O केंद्र वाले 6cm त्रिज्या वाले वृत्त की स्पर्श रेखाएँ हैं।
इसे सिद्ध करने के लिए, OQ और OR को बिंदुबद्ध रेखाओं में मिलाइए।
निर्माण से,
PQO अर्धवृत्त में एक कोण है।
हम जानते हैं कि अर्धवृत्त का कोण समकोण होता है, इसलिए यह बन जाता है,
PQO = 90°
ऐसा है कि
ओक्यू पीक्यू
चूँकि OQ 6 सेमी त्रिज्या वाले वृत्त की त्रिज्या है, इसलिए PQ को वृत्त की स्पर्श रेखा ही होना चाहिए। इसी प्रकार, हम सिद्ध कर सकते हैं कि PR वृत्त की एक स्पर्श रेखा है।
इसलिए जायज है।
2. त्रिज्या 6 सेमी के संकेंद्रित वृत्त पर एक बिंदु से 4 सेमी त्रिज्या वाले वृत्त की स्पर्श रेखा की रचना कीजिए और उसकी लंबाई मापिए। वास्तविक गणना द्वारा माप को भी सत्यापित करें।
समाधान:
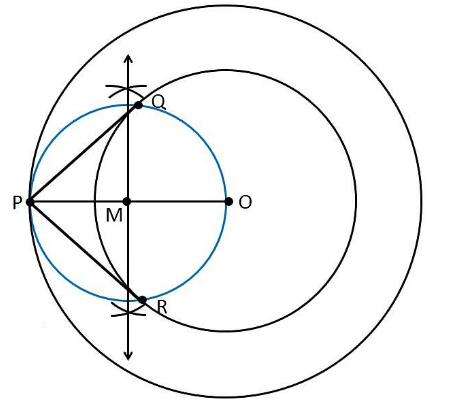
दिए गए वृत्त की स्पर्श रेखा इस प्रकार खींची जा सकती है।
1. केंद्र "O" के साथ 4 सेमी त्रिज्या का एक वृत्त बनाएं।
2. पुनः 0 को केंद्र मानकर 6 सेमी त्रिज्या का एक वृत्त खींचिए।
3. इस वृत्त पर एक बिंदु P ज्ञात कीजिए
4. बिंदुओं O और P को रेखाओं से इस प्रकार मिलाइए कि वह OP हो जाए।
5. रेखा OP . पर लम्ब समद्विभाजक खींचिए
6. मान लीजिए कि M, PO का मध्य-बिंदु है।
7. एक वृत्त खींचिए जिसका केंद्र M है और MO इसकी त्रिज्या है
8. OM त्रिज्या वाला वृत्त, दिए गए वृत्त को Q और R पर प्रतिच्छेद करता है।
9. PQ और PR को मिलाइए।
10. PQ और PR अभीष्ट स्पर्श रेखाएँ हैं।
निर्माण से, यह देखा गया है कि PQ और PR प्रत्येक की लंबाई 4.47 सेमी है।
इसकी गणना मैन्युअल रूप से निम्नानुसार की जा सकती है
PQO में,
चूँकि PQ एक स्पर्श रेखा है,
PQO = 90°। पीओ = 6 सेमी और क्यूओ = 4 सेमी
PQO में पाइथागोरस प्रमेय को लागू करने पर, हम PQ 2 +QO 2 = PQ 2 प्राप्त करते हैं
पीक्यू 2 + (4) 2 = (6) 2
पीक्यू 2 +16 = 36
पीक्यू 2 = 36−16
पीक्यू 2 = 20
पीक्यू = 2√5
पीक्यू = 4.47 सेमी
अत: स्पर्श रेखा की लंबाई PQ = 4.47
औचित्य:
दी गई समस्या की रचना को यह सिद्ध करके न्यायोचित ठहराया जा सकता है कि PQ और PR, O केंद्र वाले 4 सेमी त्रिज्या वाले वृत्त की स्पर्श रेखाएँ हैं।
इसे सिद्ध करने के लिए, OQ और OR को बिंदुबद्ध रेखाओं में मिलाइए।
निर्माण से,
PQO अर्धवृत्त में एक कोण है।
हम जानते हैं कि अर्धवृत्त का कोण समकोण होता है, इसलिए यह बन जाता है,
PQO = 90°
ऐसा है कि
ओक्यू पीक्यू
चूँकि OQ 4 सेमी त्रिज्या वाले वृत्त की त्रिज्या है, इसलिए PQ को वृत्त की स्पर्श रेखा ही होना चाहिए। इसी प्रकार, हम सिद्ध कर सकते हैं कि PR वृत्त की एक स्पर्श रेखा है।
इसलिए जायज है।
3. त्रिज्या 3 सेमी का एक वृत्त खींचिए। इसके केंद्र से 7 सेमी की दूरी पर प्रत्येक के एक विस्तारित व्यास पर दो बिंदु P और Q लें। इन दो बिंदुओं P और Q . से वृत्त पर स्पर्श रेखाएँ खींचिए
समाधान:
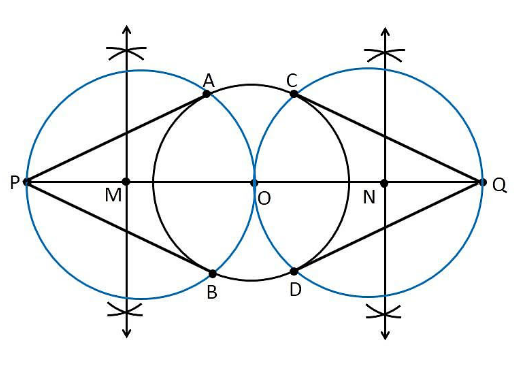
दिए गए वृत्त की स्पर्श रेखा इस प्रकार बनाई जा सकती है।
1. केंद्र "O" के साथ 3cm त्रिज्या वाला एक वृत्त खींचिए।
2. एक वृत्त का व्यास खींचिए जो केंद्र से 7 सेमी तक फैला हो और उस पर P और Q अंकित करें।
3. रेखा PO का लंब समद्विभाजक खींचिए और मध्य बिंदु को M से चिह्नित कीजिए।
4. M को केंद्र और MO को त्रिज्या लेकर एक वृत्त खींचिए
5. अब उन बिंदुओं PA और PB को मिलाइए जिनमें MO त्रिज्या वाला वृत्त 3cm वृत्त के वृत्त को प्रतिच्छेद करता है।
6. अब PA और PB अभीष्ट स्पर्श रेखाएँ हैं।
7. इसी प्रकार, बिंदु Q से हम स्पर्श रेखाएँ खींच सकते हैं।
8. उसमें से, QC और QD अभीष्ट स्पर्श रेखाएँ हैं।
औचित्य:
दी गई समस्या की रचना को यह सिद्ध करके न्यायोचित ठहराया जा सकता है कि PQ और PR, O केंद्र वाले 3 सेमी त्रिज्या वाले वृत्त की स्पर्श रेखाएँ हैं।
इसे सिद्ध करने के लिए OA और OB को मिलाइए।
निर्माण से,
PAO अर्धवृत्त में एक कोण है।
हम जानते हैं कि अर्धवृत्त का कोण समकोण होता है, इसलिए यह बन जाता है,
PAO = 90°
ऐसा है कि
ओए पीए
चूँकि OA वृत्त की त्रिज्या है जिसकी त्रिज्या 3 सेमी है, PA को वृत्त की स्पर्शरेखा ही होना चाहिए। इसी प्रकार, हम सिद्ध कर सकते हैं कि PB, QC और QD वृत्त की स्पर्श रेखाएँ हैं।
इसलिए, न्यायोचित
4. 5 सेमी त्रिज्या वाले एक वृत्त पर स्पर्श रेखाओं का एक युग्म खींचिए जो एक दूसरे से 60° के कोण पर झुकी हों
समाधान:
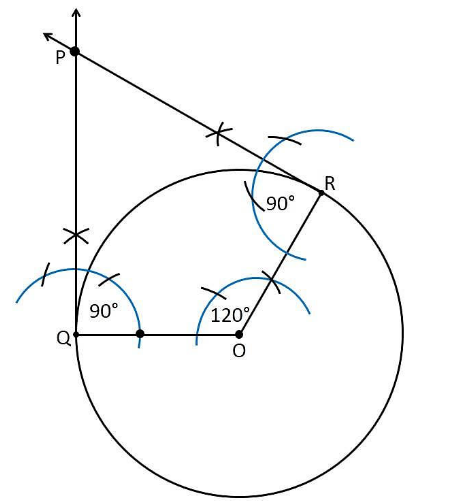
स्पर्शरेखाओं का निर्माण निम्नलिखित तरीके से किया जा सकता है:
1. त्रिज्या 5 सेमी और केंद्र 0 लेकर एक वृत्त खींचिए।
2. वृत्त की परिधि पर एक बिंदु Q लीजिए और OQ को मिलाइए।
3. QP पर बिंदु Q पर एक लंब खींचिए।
4. OQ के साथ 120° यानी (180°−60°) का कोण बनाते हुए OR त्रिज्या खींचिए।
5. बिंदु R पर RP पर एक लंब खींचिए।
6. अब दोनों लम्ब बिंदु P पर प्रतिच्छेद करते हैं।
7. इसलिए, PQ और PR 60° के कोण पर अभीष्ट स्पर्श रेखाएँ हैं।
औचित्य:
QPR = 60° . को सिद्ध करके रचना को न्यायोचित ठहराया जा सकता है
हमारे निर्माण द्वारा
OQP = 90°
ORP = 90°
और QOR = 120°
हम जानते हैं कि चतुर्भुज के सभी आंतरिक कोणों का योग = 360°
OQP+∠QOR + ∠ORP +∠QPR = 360 o
90°+120°+90°+∠QPR = 360°
इसलिए, QPR = 60°
इसलिए जायज
5. 8 सेमी लंबा एक रेखाखंड AB खींचिए। A को केंद्र मानकर, 4 सेमी त्रिज्या का एक वृत्त खींचिए और B को केंद्र मानकर 3 सेमी त्रिज्या का एक और वृत्त खींचिए। दूसरे वृत्त के केंद्र से प्रत्येक वृत्त पर स्पर्श रेखाएँ बनाइए।
समाधान:
दिए गए वृत्त की स्पर्श रेखा इस प्रकार बनाई जा सकती है।
1. एक रेखाखंड AB = 8 सेमी खींचिए।
2. A को केंद्र मानकर 4 सेमी . त्रिज्या का एक वृत्त खींचिए
3. B को केंद्र मानकर 3 cm . त्रिज्या का एक वृत्त खींचिए
4. रेखा AB का लंब समद्विभाजक खींचिए और मध्यबिंदु M लिया जाता है।
5. अब, M को केंद्र मानकर MA या MB की त्रिज्या वाला एक वृत्त खींचिए जो वृत्त को बिंदुओं P, Q, R और S पर काटता है।
6. अब एआर, एएस, बीपी और बीक्यू को मिलाएं
7. इसलिए, अभीष्ट स्पर्श रेखाएँ AR, AS, BP और BQ हैं
औचित्य:
रचना को सिद्ध करके न्यायोचित ठहराया जा सकता है कि AS और AR वृत्त की स्पर्श रेखाएँ हैं (जिसका केंद्र B है जिसकी त्रिज्या 3 सेमी है) और BP और BQ वृत्त की स्पर्श रेखाएँ हैं (जिसका केंद्र A है और त्रिज्या 4 सेमी है)।
निर्माण से, इसे साबित करने के लिए, AP, AQ, BS और BR को मिलाएँ।
ASB अर्धवृत्त में एक कोण है। हम जानते हैं कि अर्धवृत्त का कोण समकोण होता है।
ASB = 90°
बीएस एएस
चूँकि BS वृत्त की त्रिज्या है, AS को वृत्त की स्पर्श रेखा ही होना चाहिए।
इसी प्रकार, AR, BP, और BQ दिए गए वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।
6. मान लीजिए कि ABC एक समकोण त्रिभुज है जिसमें AB = 6 सेमी, BC = 8 सेमी और ∠ B = 90° है। BD, B से AC पर लम्ब है। B, C, D से होकर जाने वाला वृत्त खींचा जाता है। A से इस वृत्त पर स्पर्श रेखाएँ बनाइए।
समाधान:
दिए गए वृत्त की स्पर्श रेखा इस प्रकार बनाई जा सकती है
1. आधार BC = 8cm . वाला रेखाखंड खींचिए
2. बिंदु B पर 90° का कोण इस प्रकार मापें कि ∠ B = 90° हो।
3. B को केंद्र मानकर 6cm माप का एक चाप खींचिए।
4. मान लीजिए बिंदु A है जहां चाप किरण को काटता है।
5. लाइन AC को मिलाइए।
6. अत: ABC अभीष्ट त्रिभुज है।
7. अब, रेखा BC पर लंब समद्विभाजक खींचिए और मध्यबिंदु E के रूप में अंकित है।
8. E को केंद्र मानकर BE या EC को त्रिज्या लेकर एक वृत्त खींचिए।
9. वृत्त के मध्य बिंदु E से A को मिलाइए
10. अब, रेखा AE पर फिर से लंब समद्विभाजक खींचिए और मध्यबिंदु को M मान लिया जाता है
11. M को केंद्र के रूप में लें और AM या ME को त्रिज्या के रूप में मापें, एक वृत्त बनाएं।
12. यह वृत्त पिछले वृत्त को बिंदुओं B और Q . पर प्रतिच्छेद करता है
13. बिंदुओं A और Q को मिलाइए
14. इसलिए, AB और AQ अभीष्ट स्पर्श रेखाएँ हैं
औचित्य:
रचना को सिद्ध करके उचित ठहराया जा सकता है कि AG और AB वृत्त की स्पर्श रेखाएँ हैं।
निर्माण से, EQ में शामिल हों।
AQE अर्धवृत्त में एक कोण है। हम जानते हैं कि अर्धवृत्त का कोण समकोण होता है।
AQE = 90°
ईक्यू⊥ एक्यू
चूँकि EQ वृत्त की त्रिज्या है, AQ को वृत्त की स्पर्श रेखा होना चाहिए। इसी प्रकार, B = 90°
एबी बीई
चूँकि BE वृत्त की त्रिज्या है, AB को वृत्त की स्पर्श रेखा होना चाहिए।
इसलिए जायज है।
7. चूड़ी की सहायता से एक वृत्त खींचिए। वृत्त के बाहर एक बिंदु लीजिए। इस बिंदु से वृत्त पर स्पर्श रेखाओं के युग्म की रचना कीजिए।
समाधान:
दिए गए वृत्त पर आवश्यक स्पर्श रेखाएँ निम्नानुसार बनाई जा सकती हैं।
1. चूड़ी की सहायता से एक वृत्त खींचिए।
2. दो गैर-समानांतर जीवाएँ खींचिए जैसे AB और CD
3. AB और CD का लम्ब समद्विभाजक खींचिए
4. केंद्र को O मान लें, जहां पर लंब समद्विभाजक प्रतिच्छेद करता है।
5. स्पर्श रेखाएँ खींचने के लिए वृत्त के बाहर एक बिंदु P लीजिए।
6. बिंदुओं O और P को मिलाइए।
7. अब रेखा PO का लंब समद्विभाजक खींचिए और मध्यबिंदु को M लिया जाता है
8. M को केंद्र और MO को त्रिज्या लेकर एक वृत्त खींचिए।
9. मान लीजिए कि वृत्त वृत्त को बिंदु Q और R' पर प्रतिच्छेद करता है
10. अब PQ और PR को मिलाइए
11. इसलिए, PQ और PR अभीष्ट स्पर्श रेखाएँ हैं।
औचित्य:
निर्माण को सिद्ध करके उचित ठहराया जा सकता है कि PQ और PR वृत्त की स्पर्श रेखाएँ हैं।
चूँकि O एक वृत्त का केंद्र है, हम जानते हैं कि जीवाओं का लम्ब समद्विभाजक केंद्र से होकर गुजरता है।
अब, बिंदुओं OQ और OR को मिलाइए।
हम जानते हैं कि जीवा का लम्ब समद्विभाजक केंद्र से होकर गुजरता है।
यह स्पष्ट है कि इन लंबवत समद्विभाजकों का प्रतिच्छेदन बिंदु वृत्त का केंद्र है।
चूँकि, PQO अर्धवृत्त में एक कोण है। हम जानते हैं कि अर्धवृत्त का कोण समकोण होता है।
PQO = 90°
ओक्यू पीक्यू
चूँकि OQ वृत्त की त्रिज्या है, PQ को वृत्त की स्पर्श रेखा होना चाहिए। इसी तरह,
PRO = 90°
या पीओ
चूँकि OR वृत्त की त्रिज्या है, PR को वृत्त की स्पर्श रेखा होना चाहिए
इसलिए, PQ और PR एक वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।
![[Mathematics - X Notes]* Ncert Mathematics Class - X | Chapter 1. वास्तविक संख्या In Hindi](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgEN1UlWgqnFttBsx_dVa5f0uKAFIF9T2fyuc29IOSblF32yR0MPdnNX18wkxJnHX4tv67Ul9h-5YTY98sHsPlbK3bU00gKnl0URKEkIFUGWjA8SAY8TyxpZ9ZZMDS-XYQpag6ymKAn-_zQCamZG4vQ-zGq370Q7nMNNlh6UI4_BSuGGiYmevkFTwAQ/w680/20220223_124029.png)
![[Mathematics - X Notes]* Ncert Mathematics Class - X | Chapter 2. बहुपद In Hindi](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiXsiikGUINI-i6c1s4dNucHy3sSrwZ5ipZub1DIRn2m8MizG6YQHp67wTpnY-Uro7tM1nth6A-DKK6fbD1Q6BiMlkxhpnhXiJCsEpaSlu1dxt64zCXz6V0pMHONB6ytCpGi6p_zpGzsvVCeUK7lwBZW20xPLqWlmJlg7HHRyZKIBRzbpvlqwqZFMCD/w680/20220223_124029.png)
