एनसीईआरटी सोलूशन्स क्लास 10 गणित चैप्टर 1 वास्तविक संख्याएँ यहाँ दी गई हैं। ये समाधान हमारे विशेषज्ञ संकायों द्वारा छात्रों को उनकी पहली अवधि की परीक्षा की तैयारी में मदद करने के लिए तैयार किए गए हैं। वे गणित के लिए एनसीईआरटी समाधान हल करते हैं और प्रदान करते हैं ताकि छात्रों को समस्याओं को आसानी से हल करने में सहायता मिल सके। वे इस तरह से समाधान तैयार करने पर भी ध्यान केंद्रित करते हैं कि छात्रों के लिए इसे समझना आसान हो। वे NCERT पुस्तकों के अभ्यास में दिए गए प्रश्नों के प्रत्येक उत्तर का विस्तृत और चरणबद्ध विवरण प्रदान करते हैं।
एनसीईआरटी कक्षा 10 के गणित समाधान के पहले अध्याय में वास्तविक संख्याओं में मौजूद प्रश्नों के उत्तर दिए गए हैं । यहां, छात्रों को कई महत्वपूर्ण अवधारणाओं से परिचित कराया जाता है जो उन लोगों के लिए उपयोगी होंगे जो अपनी कक्षा 11 में गणित को एक विषय के रूप में आगे बढ़ाना चाहते हैं। एनसीईआरटी के इन समाधानों के आधार पर, छात्र अपने आगामी पहले कार्यकाल की तैयारी कर सकते हैं। ये समाधान मददगार हैं क्योंकि यह 2021-22 के लिए सीबीएसई पाठ्यक्रम की अवधि के अनुसार है।
एनसीईआरटी कक्षा 10 गणित अध्याय 1 के उत्तर तक पहुंचें - वास्तविक संख्याएं
Exercise - 1.1 पृष्ठ: 7
1. निम्नलिखित का HCF ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए:
I. 135 और 225
ii. 196 और 38220
iii. 867 और 255
समाधान:
मै। 135 और 225
जैसा कि आप देख सकते हैं, प्रश्न से 225 135 से बड़ा है। इसलिए, यूक्लिड के विभाजन एल्गोरिथ्म द्वारा, हमारे पास है,
225 = 135 × 1 + 90
अब, शेष 90 0, इस प्रकार फिर से 90 के लिए विभाजन प्रमेयिका का प्रयोग करते हुए, हम प्राप्त करते हैं,
135 = 90 × 1 + 45
फिर से, 45 0, उपरोक्त चरण को 45 के लिए दोहराते हुए, हम प्राप्त करते हैं,
90 = 45 × 2 + 0
शेष अब शून्य है, इसलिए हमारी विधि यहीं रुक जाती है। चूंकि, अंतिम चरण में, भाजक 45 है, इसलिए, HCF (225,135) = HCF (135, 90) = HCF (90, 45) = 45।
अत: 225 और 135 का HCF 45 है।
ii. 196 और 38220
इस दिए गए प्रश्न में, 38220>196, इसलिए यूक्लिड के विभाजन एल्गोरिथ्म को लागू करने और 38220 को भाजक के रूप में लेने पर, हम प्राप्त करते हैं,
38220 = 196 × 195 + 0
हमें यहाँ शेषफल 0 के रूप में पहले ही मिल चुका है। इसलिए, एचसीएफ(196, 38220) = 196।
अत: 196 और 38220 का HCF 196 है।
iii. 867 और 255
जैसा कि हम जानते हैं, 867 255 से बड़ा है। आइए अब 867 पर यूक्लिड के विभाजन एल्गोरिथ्म को लागू करें, प्राप्त करने के लिए,
867 = 255 × 3 + 102
शेष 102 0, इसलिए 255 को भाजक के रूप में लेते हुए और विभाजन प्रमेयिका विधि को लागू करने पर, हम प्राप्त करते हैं,
255 = 102 × 2 + 51
पुन: 51 0. अब 102 नया भाजक है, इसलिए उसी चरण को दोहराने से हमें प्राप्त होता है,
102 = 51 × 2 + 0
शेष अब शून्य है, इसलिए हमारी प्रक्रिया यहीं रुक जाती है। चूंकि, अंतिम चरण में, भाजक 51 है, इसलिए, एचसीएफ (867,255) = एचसीएफ (255,102) = एचसीएफ (102,51) = 51।
अत: 867 और 255 का HCF 51 है।
2. दिखाएँ कि कोई भी धनात्मक विषम पूर्णांक 6q + 1, या 6q + 3, या 6q + 5 के रूप का होता है, जहाँ q कोई पूर्णांक है।
समाधान:
मान लीजिए a कोई धनात्मक पूर्णांक है और b = 6. फिर, यूक्लिड के एल्गोरिथ्म द्वारा, a = 6q + r, किसी पूर्णांक q 0 के लिए, और r = 0, 1, 2, 3, 4, 5, क्योंकि 0≤r< 6.
अब r के मान को प्रतिस्थापित करने पर, हम प्राप्त करते हैं,
यदि r = 0, तो a = 6q
इसी प्रकार, r= 1, 2, 3, 4 और 5 के लिए, a का मान क्रमशः 6q+1, 6q+2, 6q+3, 6q+4 और 6q+5 है।
यदि a = 6q, 6q+2, 6q+4, तो a एक सम संख्या है और 2 से विभाज्य है। एक धनात्मक पूर्णांक सम या विषम हो सकता है। इसलिए, कोई भी धनात्मक विषम पूर्णांक 6q+1, 6q+ के रूप का होता है। 3 और 6q+5, जहाँ q कोई पूर्णांक है।
3. 616 सदस्यों की सेना की टुकड़ी को परेड में 32 सदस्यों के सेना बैंड के पीछे मार्च करना है। दोनों समूहों को समान संख्या में कॉलम में मार्च करना है। कॉलम की अधिकतम संख्या क्या है जिसमें वे मार्च कर सकते हैं?
समाधान:
दिया गया,
सेना के दल के सदस्यों की संख्या=616
सेना बैंड के सदस्यों की संख्या = 32
यदि दो समूहों को एक ही कॉलम में चलना है, तो हमें दो समूहों के बीच उच्चतम सामान्य कारक का पता लगाना होगा। एचसीएफ (616, 32), अधिकतम कॉलम देता है जिसमें वे मार्च कर सकते हैं।
यूक्लिड के एल्गोरिदम का उपयोग करके उनके एचसीएफ को खोजने के लिए, हम प्राप्त करते हैं,
चूंकि, 616>32, इसलिए,
616 = 32 × 19 + 8
चूँकि, 8 0, इसलिए, 32 को नया भाजक के रूप में लेते हुए, हमारे पास है,
32 = 8 × 4 + 0
अब हमें 0 के रूप में शेषफल मिला है, इसलिए, एचसीएफ (616, 32) = 8।
इसलिए, स्तंभों की अधिकतम संख्या जिसमें वे मार्च कर सकते हैं, 8 है।
4. यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का वर्ग किसी पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता है।
समाधान:
मान लीजिए x कोई धनात्मक पूर्णांक है और y = 3 है।
यूक्लिड विभाजन एल्गोरिथ्म द्वारा, तब,
x = 3q + r किसी पूर्णांक q≥0 के लिए और r = 0, 1, 2, r 0 और r <3 के रूप में।
इसलिए, x = 3q, 3q+1 और 3q+2
अब दिए गए प्रश्न के अनुसार, दोनों पक्षों का वर्ग करने पर, हम प्राप्त करते हैं,
x 2 = (3q) 2 = 9q 2 = 3 × 3q 2
माना 3q 2 = m
इसलिए, x 2 = 3m ………………..(1)
x 2 = (3q + 1) 2 = (3q) 2 +1 2 +2×3q×1 = 9q 2 + 1 +6q = 3(3q 2 +2q) +1
प्राप्त करने के लिए , 3q 2 +2q = m को प्रतिस्थापित कीजिए।
x 2 = 3मी + 1 ……………………………. (2)
x 2 = (3q + 2) 2 = (3q) 2 +2 2 +2×3q×2 = 9q 2 + 4 + 12q = 3 (3q 2 + 4q + 1)+1
पुनः, प्राप्त करने के लिए, 3q 2 +4q+1 = m प्रतिस्थापित कीजिए,
x 2 = 3मी + 1…………………………(3)
इसलिए, समीकरण 1, 2 और 3 से, हम कह सकते हैं कि, किसी भी धनात्मक पूर्णांक का वर्ग या तो 3m के रूप में होता है या किसी पूर्णांक m के लिए 3m + 1 के रूप में।
5. यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का घन 9m, 9m + 1 या 9m + 8 के रूप का होता है।
समाधान:
मान लीजिए x कोई धनात्मक पूर्णांक है और y = 3 है।
यूक्लिड विभाजन एल्गोरिथ्म द्वारा, तब,
x = 3q+r, जहाँ q≥0 और r = 0, 1, 2, r 0 और r <3 के रूप में।
इसलिए, r का मान रखने पर, हमें प्राप्त होता है,
एक्स = 3q
या
एक्स = 3q + 1
या
एक्स = 3q + 2
अब, उपरोक्त तीनों भावों का घन लेने पर, हम प्राप्त करते हैं,
स्थिति (i): जब r = 0, तब,
x 2 = (3q) 3 = 27q 3 = 9(3q 3 )= 9m; जहां एम = 3q 3
स्थिति (ii): जब r = 1, तब,
x 3 = (3q+1) 3 = (3q) 3 +1 3 +3×3q×1(3q+1) = 27q 3 +1+27q 2 +9q
9 को सामान्य गुणनखंड के रूप में लेते हुए, हम प्राप्त करते हैं,
x 3 = 9(3q 3 +3q 2 +q)+1
लगाना = मी, हम पाते हैं,
(3q 3 +3q 2+ q) = m रखने पर, हम पाते हैं,
एक्स 3 = 9मी+1
स्थिति (iii): जब r = 2, तब,
x 3 = (3q+2) 3 = (3q) 3 +2 3 +3×3q×2(3q+2) = 27q 3 +54q 2 +36q+8
9 को सामान्य गुणनखंड के रूप में लेते हुए, हम प्राप्त करते हैं,
x 3 =9(3q 3 +6q 2 +4q)+8
(3q 3 +6q 2 +4q) = m रखने पर, हम पाते हैं,
एक्स 3 = 9मी+8
अतः ऊपर वर्णित तीनों स्थितियों से यह सिद्ध होता है कि किसी धनात्मक पूर्णांक का घन 9m, 9m + 1 या 9m + 8 के रूप का होता है।
Exercise - 1.2 पृष्ठ: 11
1. प्रत्येक संख्या को उसके अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
समाधान:
(i) 140
140 का LCM लेने पर हमें इसके अभाज्य गुणनखंड का गुणनफल प्राप्त होगा।
इसलिए, 140 = 2 × 2 × 5 × 7 × 1 = 2 2 ×5×7
(ii) 156
156 का LCM लेने पर हमें इसके अभाज्य गुणनखंड का गुणनफल प्राप्त होगा।
अत: 156 = 2 × 2 × 13 × 3 × 1 = 2 2 × 13 × 3
(iii) 3825
3825 का LCM लेने पर हमें इसके अभाज्य गुणनखंड का गुणनफल प्राप्त होगा।
अत: 3825 = 3 × 3 × 5 × 5 × 17 × 1 = 3 2 × 5 2 × 17
(iv) 5005
5005 का LCM लेने पर हमें इसके अभाज्य गुणनखंड का गुणनफल प्राप्त होगा।
अत: 5005 = 5 × 7 × 11 × 13 × 1 = 5 × 7 × 11 × 13
(v) 7429
7429 का LCM लेने पर हमें इसके अभाज्य गुणनखंड का गुणनफल प्राप्त होगा।
अत: 7429 = 17 × 19 × 23 × 1 = 17 × 19 × 23
2. पूर्णांकों के निम्नलिखित युग्मों का LCM और HCF ज्ञात कीजिए और सत्यापित कीजिए कि LCM × HCF = दो संख्याओं का गुणनफल।
(i) 26 और 91
(ii) 510 और 92
(iii) 336 और 54
समाधान:
(i) 26 और 91
26 और 91 को इसके अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त करने पर, हम प्राप्त करते हैं,
26 = 2 × 13 × 1
91 = 7 × 13 × 1
इसलिए, एलसीएम (26, 91) = 2 × 7 × 13 × 1 = 182
और एचसीएफ (26, 91) = 13
सत्यापन
अब, 26 और 91 का गुणनफल = 26 × 91 = 2366
और एलसीएम और एचसीएफ का गुणनफल = 182 × 13 = 2366
अत: LCM × HCF = 26 और 91 का गुणनफल।
(ii) 510 और 92
510 और 92 को इसके अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त करने पर, हम प्राप्त करते हैं,
510 = 2 × 3 × 17 × 5 × 1
92 = 2 × 2 × 23 × 1
इसलिए, एलसीएम (510, 92) = 2 × 2 × 3 × 5 × 17 × 23 = 23460
और एचसीएफ (510, 92) = 2
सत्यापन
अब, 510 और 92 का गुणनफल = 510 × 92 = 46920
और एलसीएम और एचसीएफ का गुणनफल = 23460 × 2 = 46920
अत: LCM × HCF = 510 और 92 का गुणनफल।
(iii) 336 और 54
336 और 54 को इसके अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त करने पर, हम प्राप्त करते हैं,
336 = 2 × 2 × 2 × 2 × 7 × 3 × 1
54 = 2 × 3 × 3 × 3 × 1
इसलिए, एलसीएम(336, 54) = = 3024
और एचसीएफ(336, 54) = 2×3 = 6
सत्यापन
अब, 336 और 54 का गुणनफल = 336 × 54 = 18,144
और एलसीएम और एचसीएफ का गुणनफल = 3024 × 6 = 18,144
अत: LCM × HCF = 336 और 54 का गुणनफल।
3. अभाज्य गुणनखंडन विधि को लागू करके निम्नलिखित पूर्णांकों का LCM और HCF ज्ञात कीजिए।
(i) 12, 15 और 21
(ii) 17, 23 और 29
(iii) 8, 9 और 25
समाधान:
(i) 12, 15 और 21
तीनों संख्याओं के अभाज्य गुणनखंडों का गुणनफल लिखने पर, हम प्राप्त करते हैं,
12=2×2×3
15=5×3
21=7×3
इसलिए,
एचसीएफ(12,15,21) = 3
एलसीएम(12,15,21) = 2 × 2 × 3 × 5 × 7 = 420
(ii) 17, 23 और 29
तीनों संख्याओं के अभाज्य गुणनखंडों का गुणनफल लिखने पर, हम प्राप्त करते हैं,
17=17×1
23=23×1
29=29×1
इसलिए,
एचसीएफ (17,23,29) = 1
एलसीएम (17,23,29) = 17 × 23 × 29 = 11339
(iii) 8, 9 और 25
तीनों संख्याओं के अभाज्य गुणनखंडों का गुणनफल लिखने पर, हम प्राप्त करते हैं,
8=2×2×2×1
9=3×3×1
25=5×5×1
इसलिए,
एचसीएफ(8,9,25)=1
एलसीएम(8,9,25) = 2×2×2×3×3×5×5 = 1800
4. दिया गया है कि HCF (306, 657) = 9, LCM (306, 657) ज्ञात कीजिए।
हल: जैसा कि हम जानते हैं कि,
HCF×LCM=दो दी गई संख्याओं का गुणनफल
इसलिए,
9 × एलसीएम = 306 × 657
एलसीएम = (306×657)/9 = 22338
इसलिए, एलसीएम(306,657) = 22338
5. जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए 6 n अंक 0 पर समाप्त हो सकता है।
हल: यदि संख्या 6 n अंक शून्य (0) के साथ समाप्त होती है, तो यह 5 से विभाज्य होनी चाहिए, क्योंकि हम जानते हैं कि कोई भी संख्या जिसका इकाई स्थान 0 या 5 है, वह 5 से विभाज्य है।
6 n = (2×3) n . का अभाज्य गुणनखंडन
इसलिए, 6 n के अभाज्य गुणनखंड में अभाज्य संख्या 5 नहीं है।
इसलिए, यह स्पष्ट है कि किसी भी प्राकृतिक संख्या n के लिए, 6 n 5 से विभाज्य नहीं है और इस प्रकार यह साबित होता है कि किसी भी प्राकृतिक संख्या n के लिए 6 n अंक 0 पर समाप्त नहीं हो सकता है।
6. समझाइए कि 7 × 11 × 13 + 13 और 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 भाज्य संख्याएँ क्यों हैं।
हल: भाज्य संख्या की परिभाषा के अनुसार, हम जानते हैं कि यदि कोई संख्या भाज्य है, तो इसका अर्थ है कि उसके 1 और स्वयं के अलावा अन्य गुणनखंड हैं। इसलिए, दिए गए व्यंजक के लिए;
7 × 11 × 13 + 13
सामान्य गुणनखंड के रूप में 13 लेते हुए, हम प्राप्त करते हैं,
=13(7×11×1+1) = 13(77+1) = 13×78 = 13×3×2×13
अत: 7 × 11 × 13 + 13 एक भाज्य संख्या है।
अब दूसरा नंबर लेते हैं,
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
5 को एक उभयनिष्ठ गुणनखंड के रूप में लेने पर, हम प्राप्त करते हैं,
=5(7×6×4×3×2×1+1) = 5(1008+1) = 5×1009
अत: 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 एक भाज्य संख्या है।
7. एक खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। सोनिया को मैदान का एक चक्कर लगाने में 18 मिनट लगते हैं, जबकि रवि को इसके लिए 12 मिनट लगते हैं। मान लीजिए कि वे दोनों एक ही बिंदु पर और एक ही समय पर चलना शुरू करते हैं और एक ही दिशा में जाते हैं। कितने मिनट बाद वे फिर से शुरुआती बिंदु पर मिलेंगे?
हल: चूँकि सोनिया और रवि दोनों एक ही दिशा में और एक ही समय पर चलते हैं, इसलिए समय निकालने की विधि जब वे फिर से शुरुआती बिंदु पर मिलेंगे, 18 और 12 का LCM है।
इसलिए, एलसीएम(18,12) = 2×3×3×2×1=36
अतः सोनिया और रवि 36 मिनट के बाद फिर से शुरुआती बिंदु पर मिलेंगे।
Exercise - 1.3 पृष्ठ: 14
1. सिद्ध कीजिए कि 5 अपरिमेय है।
हल: मान लीजिए कि 5 एक परिमेय संख्या है।
यानी 5 = x/ y (जहाँ, x और y सह-अभाज्य हैं)
वाई 5 = एक्स
दोनों पक्षों का वर्ग करने पर, हम प्राप्त करते हैं,
(वाई √ 5) 2 = एक्स 2
5y 2 = x 2 ……………………….. (1)
अत: x 2 5 से विभाज्य है, इसलिए x भी 5 से विभाज्य है।
मान लीजिए, x = 5k, k के कुछ मान के लिए और x के मान को समीकरण (1) में प्रतिस्थापित करने पर, हम प्राप्त करते हैं,
5y 2 = (5k) 2
y 2 = 5k 2
5 से विभाज्य है इसका अर्थ है कि y 5 से विभाज्य है।
स्पष्ट रूप से, x और y सह-अभाज्य नहीं हैं। इस प्रकार, 5 के बारे में हमारी धारणा परिमेय है गलत है।
अतः 5 एक अपरिमेय संख्या है।
2. सिद्ध कीजिए कि 3 + 2√5 + अपरिमेय है।
हल: मान लीजिए कि 3 + 2 5 परिमेय है।
तब हम सह-अभाज्य x और y (y ≠ 0) इस प्रकार ज्ञात कर सकते हैं कि 3 + 2√5 = x/y
पुनर्व्यवस्थित, हम प्राप्त करते हैं,
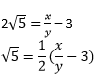
चूँकि, x और y पूर्णांक हैं, इस प्रकार,
 एक परिमेय संख्या है।
एक परिमेय संख्या है।
अतः 5 भी एक परिमेय संख्या है। लेकिन यह इस तथ्य का खंडन करता है कि 5 अपरिमेय है ।
अतः, हम यह निष्कर्ष निकालते हैं कि 3 + 2 5 अपरिमेय है।
3. सिद्ध कीजिए कि निम्नलिखित अपरिमेय हैं:
(i) 1/√2
(ii) 7√5
(iii) 6 + 2
समाधान:
(i) 1 / 2
आइए मान लें कि 1/√2 तर्कसंगत है।
तब हम सह-अभाज्य x और y (y ≠ 0) इस प्रकार ज्ञात कर सकते हैं कि 1/√2 = x/y
पुनर्व्यवस्थित, हम प्राप्त करते हैं,
√2 = वाई/एक्स
चूँकि, x और y पूर्णांक हैं, अत: √2 एक परिमेय संख्या है, जो इस तथ्य का खंडन करती है कि √2 अपरिमेय है।
इसलिए, हम यह निष्कर्ष निकाल सकते हैं कि 1/√2 अपरिमेय है।
(ii) 7 5
मान लीजिए कि 7√5 एक परिमेय संख्या है।
तब हम सह-अभाज्य a और b (b ≠ 0) इस प्रकार प्राप्त कर सकते हैं कि 7√5 = x/y
पुनर्व्यवस्थित, हम प्राप्त करते हैं,
5 = x/7y
चूँकि, x और y पूर्णांक हैं, इस प्रकार, 5 एक परिमेय संख्या है, जो इस तथ्य का खंडन करती है कि √5 अपरिमेय है।
अतः, हम यह निष्कर्ष निकाल सकते हैं कि 7√5 अपरिमेय है।
(iii) 6 + 2
मान लीजिए कि 6 +√2 एक परिमेय संख्या है।
तब हम सह-अभाज्य x और y (y ≠ 0) इस प्रकार ज्ञात कर सकते हैं कि 6 +√2 = x/y⋅
पुनर्व्यवस्थित, हम प्राप्त करते हैं,
2 = (एक्स/वाई) - 6
चूँकि, x और y पूर्णांक हैं, इस प्रकार (x/y) - 6 एक परिमेय संख्या है और इसलिए, 2 परिमेय संख्या है। यह इस तथ्य का खंडन करता है कि √2 एक अपरिमेय संख्या है।
अतः, हम यह निष्कर्ष निकाल सकते हैं कि 6 +√2 अपरिमेय है।
Exercise - 1.4 पृष्ठ: 17
1. वास्तव में लंबे विभाजन को निष्पादित किए बिना, बताएं कि क्या निम्नलिखित परिमेय संख्याओं का एक सांत दशमलव विस्तार होगा या एक गैर-सांत दोहराव वाला दशमलव विस्तार होगा:
(i) 13/3125 (ii) 17/8 (iii) 64/455 (iv) 15/1600 (v) 29/343 (vi) 23/(2 3 5 2 ) (vii) 129/(2 2 5 7 7 5 ) (viii) 6/15 (ix) 35/50 (x) 77/210
समाधान:
नोट: यदि हर में केवल 2 और 5 के गुणनखंड हों या 2 m ×5 n के रूप में हों, तो इसका दशमलव प्रसार सांत होता है।
यदि हर में 2 और 5 के अलावा अन्य गुणनखंड हों तो उसका दशमलव प्रसार असांत होता है।
(i) 13/3125
हर का गुणनखंड करना, हम प्राप्त करते हैं,
3125 = 5 × 5 × 5 × 5 × 5 = 5 5
चूंकि, हर का गुणनखंड केवल 5 है, 13/3125 का दशमलव प्रसार सांत है।
(ii) 17/8
हर का गुणनखंड करना, हम प्राप्त करते हैं,
8 = 2×2×2 = 2 3
चूंकि, हर का गुणनखंड केवल 2 होता है, 17/8 का दशमलव प्रसार सांत होता है।
(iii) 64/455
हर का गुणनखंड करना, हम प्राप्त करते हैं,
455 = 5×7×13
चूँकि हर 2 m × 5 n के रूप में नहीं है , इस प्रकार 64/455 का दशमलव प्रसार असांत है।
(iv) 15/1600
हर का गुणनखंड करना, हम प्राप्त करते हैं,
1600 = 2 6 × 5 2
चूँकि हर 2 m × 5 n के रूप में है, इस प्रकार 15/1600 का दशमलव प्रसार सांत है।
(v) 29/343
हर का गुणनखंड करना, हम प्राप्त करते हैं,
343 = 7×7×7 = 7 3 चूँकि, हर 2 m × 5 n के रूप में नहीं है, इसलिए 29/343 का दशमलव प्रसार असांत है।
(vi) 23/(2 3 5 2 )
स्पष्ट है कि हर 2 m × 5 n के रूप में है ।
इसलिए, 23/ (2 3 5 2 ) का एक सांत दशमलव प्रसार है।
(vii) 129/(2 2 5 7 7 5 )
जैसा कि आप देख सकते हैं, हर 2 m × 5 n के रूप में नहीं है ।
अत: 129/ (2 2 5 7 7 5 ) का दशमलव प्रसार असांत है।
(viii) 6/15
6/15 = 2/5
चूँकि हर का गुणनखंड केवल 5 है, इस प्रकार, 6/15 का दशमलव प्रसार सांत है।
(ix) 35/50
35/50 = 7/10
हर का गुणनखंड करना, हम प्राप्त करते हैं,
10 = 2 × 5
चूँकि हर 2 m × 5 n के रूप में है, इसलिए 35/50 का दशमलव प्रसार सांत है।
(एक्स) 77/210
77/210 = (7× 11)/ (30 × 7) = 11/30
हर का गुणनखंड करना, हम प्राप्त करते हैं,
30 = 2 × 3 × 5
जैसा कि आप देख सकते हैं, हर 2 m × 5 n के रूप में नहीं है। इसलिए, 77/210 का दशमलव प्रसार असांत है।
2. ऊपर दिए गए प्रश्न 1 में उन परिमेय संख्याओं के दशमलव प्रसार लिखिए जिनमें सांत दशमलव प्रसार हैं।
समाधान:
(i) 13/3125

13/3125 = 0.00416
(ii) 17/8
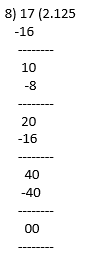
17/8 = 2.125
(iii) 64/455 का दशमलव प्रसार असांत है
(iv)15/1600

15/1600 = 0.009375
(v) 29/343 का दशमलव प्रसार असांत है
(vi)23/ (2 3 5 2 ) = 23/(8×25)= 23/200

23/ (2 3 5 2 ) = 0.115
(vii) 129/ (2 2 5 7 7 5 ) का दशमलव प्रसार असांत है
(viii) 6/15 = 2/5

(ix) 35/50 = 7/10
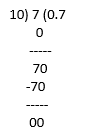
35/50 = 0.7
(x) 77/210 का दशमलव प्रसार असांत है।
3. निम्नलिखित वास्तविक संख्याओं का दशमलव प्रसार नीचे दिया गया है। प्रत्येक मामले में, तय करें कि वे तर्कसंगत हैं या नहीं। यदि वे परिमेय हैं, और pq के रूप में हैं, तो आप q के अभाज्य गुणनखंडों के बारे में क्या कह सकते हैं?
(i) 43.123456789
(ii) 0.120120012000120000। . .
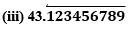
समाधान:
(i) 43.123456789
चूँकि इसका सांत दशमलव प्रसार है, यह p/q के रूप में एक परिमेय संख्या है और q में केवल 2 और 5 के गुणनखंड हैं।
(ii) 0.120120012000120000। . .
चूँकि इसका दशमलव प्रसार असांत और अनावर्ती है, इसलिए यह एक अपरिमेय संख्या है।
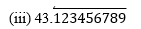
चूँकि इसमें असांत लेकिन आवर्ती दशमलव प्रसार है, यह p/q के रूप में एक परिमेय संख्या है और q में 2 और 5 के अलावा अन्य गुणनखंड हैं।









