कक्षा 10 गणित अध्याय 3 के लिए एनसीईआरटी समाधान
NCERT Solutions for Class 10 Maths Chapter 3 दो चरों में रैखिक समीकरण युग्म विद्यार्थियों को यह समझने में मदद करेगा कि इस अवधारणा के तहत समस्याओं को कैसे हल किया जाता है। गणित एक ऐसा विषय है जिसके लिए बहुत अभ्यास की आवश्यकता होती है। 10 वीं कक्षा के प्रथम और द्वितीय सत्र की परीक्षाओं में बैठने वाले छात्र संदर्भ के लिए एनसीईआरटी समाधान कक्षा 10 की ओर रुख कर सकते हैं। दो चरों में रैखिक समीकरणों के चैप्टर पेयर के ये समाधान एनसीईआरटी पाठ्यपुस्तक में गणित की सभी समस्याओं के चरण-वार उत्तर देते हैं । एक समीकरण जो ax + by + c = 0 के रूप का हो सकता है, जहाँ a, b और c वास्तविक संख्याएँ हैं, और a और b दोनों शून्य नहीं हैं, दो चर x और y में रैखिक समीकरण कहलाता है।
कक्षा 10 गणित अध्याय 3 के लिए एनसीईआरटी समाधान भी छात्रों को इस तथ्य को समझने देता है कि इस तरह के समीकरण का समाधान मानों की एक जोड़ी है, एक एक्स के लिए और दूसरा वाई के लिए, जो समीकरण के दोनों पक्षों को बराबर बनाता है। विद्यार्थी यह भी सीखते हैं कि समीकरण का प्रत्येक हल उसे निरूपित करने वाली रेखा पर एक बिंदु है।
छात्रों को 2021-22 के लिए सीबीएसई सिलेबस के पहले टर्म के दो वेरिएबल्स में लीनियर इक्वेशन के चैप्टर 3 पेयर में मौजूद प्रश्नों की समस्या-समाधान विधि सीखने को मिलती है, जो ऊपर वर्णित अवधारणाओं के इर्द-गिर्द घूमती है, नीचे दिए गए एनसीईआरटी सॉल्यूशंस का अभ्यास करके । एनसीईआरटी के ये समाधान प्रथम सत्र की परीक्षा के नजरिए से बेहद फायदेमंद हैं।
एनसीईआरटी कक्षा 10 गणित अध्याय 3 के उत्तर - दो चरों में रैखिक समीकरणों का युग्म
Exercise - 3.1 पृष्ठ: 44
1. आफताब अपनी बेटी से कहता है, “सात साल पहले, मैं उस समय आपकी उम्र का सात गुना था। इसके अलावा, अब से तीन साल बाद, मैं आपकी उम्र का तीन गुना हो जाऊंगा।” (क्या यह दिलचस्प नहीं है?) इस स्थिति को बीजगणितीय और आलेखीय रूप से निरूपित करें।
हल : माना आफताब की वर्तमान आयु 'x' है।
और, उसकी पुत्री की वर्तमान आयु 'y' है।
अब, हम लिख सकते हैं, सात साल पहले,
आफताब की आयु = x-7
उसकी पुत्री की आयु = y-7
प्रश्न के अनुसार,
x−7 = 7(y−7)
⇒x−7 = 7y−49
x−7y = −42 ………………………(i)
साथ ही, अब से तीन साल या तीन साल बाद,
आफताब की आयु = x+3 हो जाएगी।
उसकी पुत्री की आयु होगी = y+3
दी गई स्थिति के अनुसार,
एक्स+3 = 3(वाई+3)
x+3 = 3y+9
x−3y = 6 ………………………………(ii)
समीकरण (i) को समीकरण (ii) से घटाने पर हमें प्राप्त होता है
(x−3y)−(x−7y) = 6−(−42)
⇒−3y+7y = 6+42
4y = 48
y = 12
बीजीय समीकरण द्वारा दर्शाया जाता है
x−7y = −42
x−3y = 6
के लिए, x−7y = −42 या x = −42+7y
समाधान तालिका है

के लिए, x−3y = 6 या x = 6+3y
समाधान तालिका है

चित्रमय प्रतिनिधित्व है:
2. एक क्रिकेट टीम का कोच 3 बल्ले और 6 गेंदें 3900 रुपये में खरीदता है। बाद में, वह 1300 रुपये में एक और बल्ला और उसी तरह की 3 गेंदें खरीदती है। इस स्थिति को बीजगणितीय और ज्यामितीय रूप से निरूपित करें।
हल: मान लीजिए कि एक बल्ले की कीमत 'रु x' है।
और, एक गेंद की कीमत 'रुपये y' होगी।
प्रश्न के अनुसार, बीजीय निरूपण है
3x+6y = 3900
और x+3y = 1300
3x+6y = 3900 . के लिए
या x = (3900-6y)/3
समाधान तालिका है

के लिए, x+3y = 1300
या एक्स = 1300-3y
समाधान तालिका है

चित्रमय प्रतिनिधित्व इस प्रकार है।
3. एक दिन में 2 किलो सेब और 1 किलो अंगूर की कीमत 160 रुपये पाई गई। एक महीने के बाद, 4 किलो सेब और 2 किलो अंगूर की कीमत 300 रुपये है। स्थिति को बीजगणितीय और ज्यामितीय रूप से निरूपित करें।
हल: मान लीजिए कि 1 किलो सेब का मूल्य 'रु. एक्स'
और, 1 किलो अंगूर की कीमत 'रु. वाई'
प्रश्न के अनुसार, बीजीय निरूपण है
2x+y = 160
और 4x+2y = 300
2x+y = 160 या y = 160−2x के लिए, समाधान तालिका है;

4x+2y = 300 या y = (300-4x)/2 के लिए, समाधान तालिका है;

चित्रमय प्रतिनिधित्व इस प्रकार है;

Exercise - 3.2 पृष्ठ: 49
1. निम्नलिखित समस्याओं में रैखिक समीकरण युग्म बनाइए और उनके हल आलेखीय रूप से ज्ञात कीजिए।
(i) दसवीं कक्षा के 10 छात्रों ने गणित प्रश्नोत्तरी में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या से 4 अधिक है, तो प्रश्नोत्तरी में भाग लेने वाले लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
(ii) 5 पेंसिल और 7 पेन की एकसाथ कीमत 50 है, जबकि 7 पेंसिल और 5 पेन की कुल कीमत 46 है। एक पेंसिल और एक पेन की कीमत पाएं।
समाधान:
(i) माना लड़कियों की संख्या x और लड़कों की y संख्या है। दिए गए प्रश्न के अनुसार, बीजीय व्यंजक को निम्न प्रकार से दर्शाया जा सकता है।
एक्स +वाई = 10
एक्स- वाई = 4
अब, x+y = 10 या x = 10−y के लिए, समाधान हैं;

x - y = 4 या x = 4 + y के लिए, समाधान हैं;

चित्रमय प्रतिनिधित्व इस प्रकार है;

ग्राफ से यह देखा जा सकता है कि दी गई रेखाएं एक दूसरे को बिंदु (7, 3) पर काटती हैं। अत: कक्षा में 7 लड़कियां और 3 लड़के हैं।
(ii) माना 1 पेंसिल की कीमत x रुपये और 1 पेन की कीमत y रुपये है।
प्रश्न के अनुसार, बीजीय व्यंजक कैब को इस प्रकार दर्शाया जा सकता है;
5x + 7y = 50
7x + 5y = 46
5x + 7y = 50 या x = (50-7y)/5 के लिए, समाधान हैं;

7x + 5y = 46 या x = (46-5y)/7 के लिए, समाधान हैं;

इसलिए, चित्रमय प्रतिनिधित्व इस प्रकार है;

ग्राफ से यह देखा जा सकता है कि दी गई रेखाएं एक दूसरे को बिंदु (3, 5) पर काटती हैं।
तो, एक पेंसिल की कीमत 3/- है और एक पेन की कीमत 5/- है।
2. अनुपातों a1/a2 , b1/b2 , c1/c2 की तुलना करने पर पता लगाएँ कि रैखिक समीकरणों के निम्नलिखित युग्मों को निरूपित करने वाली रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर या संपाती हैं:
(i) 5x - 4y + 8 = 0
7x + 6y - 9 = 0
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x - 3y + 10 = 0
2x - y + 9 = 0
समाधान:
(i) दिए गए भाव;
5x−4y+8 = 0
7x+6y−9 = 0
इन समीकरणों की तुलना a1x+b1y+c1 = 0 . से करना
और a2x+b2y+c2 = 0
हमें मिला,
a1 = 5, b1 = -4, c1 = 8
a2 = 7, b2 = 6, c2 = -9
(ए1/ए2) = 5/7
(बी1/बी2) = -4/6 = -2/3
(सी1/सी2) = 8/-9
चूँकि, (a1/a2) (b1/b2)
अतः, प्रश्न में दिए गए समीकरणों के युग्मों का एक अनूठा हल है और रेखाएँ एक दूसरे को ठीक एक बिंदु पर काटती हैं।
(ii) दिए गए भाव;
9x + 3y + 12 = 0
18x + 6y + 24 = 0
इन समीकरणों की तुलना a1x+b1y+c1 = 0 . से करना
और a2x+b2y+c2 = 0
हमें मिला,
a1 = 9, b1 = 3, c1 = 12
a2 = 18, b2 = 6, c2 = 24
(a1/a2) = 9/18 = 1/2
(बी1/बी2) = 3/6 = 1/2
(सी1/सी2) = 12/24 = 1/2
चूँकि (a1/a2) = (b1/b2) = (c1/c2)
अतः, प्रश्न में दिए गए समीकरणों के युग्मों के अनंत संभव हल हैं और रेखाएँ संपाती हैं।
(iii) दिए गए भाव;
6x - 3y + 10 = 0
2x - y + 9 = 0
इन समीकरणों की तुलना a1x+b1y+c1 = 0 . से करना
और a2x+b2y+c2 = 0
हमें मिला,
a1 = 6, b1 = -3, c1 = 10
a2 = 2, b2 = -1, c2 = 9
(a1/a2) = 6/2 = 3/1
(बी1/बी2) = -3/-1 = 3/1
(सी1/सी2) = 10/9
चूँकि (a1/a2) = (b1/b2) ≠ (c1/c2)
अतः, प्रश्न में दिए गए समीकरणों के युग्म एक दूसरे के समानांतर हैं और रेखाएँ कभी भी एक दूसरे को किसी भी बिंदु पर नहीं काटती हैं और दिए गए समीकरणों के युग्म का कोई संभावित हल नहीं है।
3. अनुपात (a1/a2) , (b1/b2) , (c1/c2) की तुलना करने पर ज्ञात कीजिए कि निम्नलिखित रैखिक समीकरण युग्म संगत हैं या असंगत।
(i) 3x + 2y = 5; 2x - 3y = 7
(ii) 2x - 3y = 8; 4x - 6y = 9
(iii)(3/2)x+(5/3)y = 7; 9x - 10y = 14
(iv) 5x - 3y = 11; - 10x + 6y = -22
(v)(4/3)x+2y = 8; 2x + 3y = 12
समाधान:
(i) दिया गया है : 3x + 2y = 5 या 3x + 2y -5 = 0
और 2x - 3y = 7 या 2x - 3y -7 = 0
इन समीकरणों की तुलना a1x+b1y+c1 = 0 . से करना
और a2x+b2y+c2 = 0
हमें मिला,
a1 = 3, b1 = 2, c1 = -5
a2 = 2, b2 = -3, c2 = -7
(ए1/ए2) = 3/2
(बी1/बी2) = 2/-3
(c1/c2) = -5/-7 = 5/7
चूँकि, (a1/a2) (b1/b2)
अतः दिए गए समीकरण एक दूसरे को एक बिंदु पर प्रतिच्छेद करते हैं और उनका केवल एक ही संभावित हल है। समीकरण सुसंगत हैं।
(ii) दिया गया है 2x - 3y = 8 और 4x - 6y = 9
इसलिए,
a1 = 2, b1 = -3, c1 = -8
a2 = 4, b2 = -6, c2 = -9
(a1/a2) = 2/4 = 1/2
(बी1/बी2) = -3/-6 = 1/2
(c1/c2) = -8/-9 = 8/9
चूँकि , (a1/a2) = (b1/b2) ≠ (c1/c2)
इसलिए, समीकरण एक दूसरे के समानांतर हैं और उनका कोई संभावित हल नहीं है। इसलिए, समीकरण असंगत हैं।
(iii) दिया गया है (3/2)x + (5/3)y = 7 और 9x - 10y = 14
इसलिए,
a1 = 3/2, b1 = 5/3, c1 = -7
a2 = 9, b2 = -10, c2 = -14
(a1/a2) = 3/(2×9) = 1/6
(बी1/बी2) = 5/(3× -10)= -1/6
(c1/c2) = -7/-14 = 1/2
चूँकि, (a1/a2) (b1/b2)
अतः समीकरण एक दूसरे को एक बिंदु पर प्रतिच्छेद कर रहे हैं और उनका केवल एक ही संभावित हल है। इसलिए, समीकरण सुसंगत हैं।
(iv) दिया गया है, 5x - 3y = 11 और - 10x + 6y = -22
इसलिए,
a1 = 5, b1 = -3, c1 = -11
a2 = -10, b2 = 6, c2 = 22
(a1/a2) = 5/(-10) = -5/10 = -1/2
(बी1/बी2) = -3/6 = -1/2
(c1/c2) = -11/22 = -1/2
चूँकि (a1/a2) = (b1/b2) = (c1/c2)
ये रैखिक समीकरण संपाती रेखाएं हैं और इनके अनंत संभव समाधान हैं। इसलिए, समीकरण सुसंगत हैं।
(v)दिया गया है, (4/3)x +2y = 8 और 2x + 3y = 12
a1 = 4/3 , b1= 2 , c1 = -8
a2 = 2, b2 = 3, c2 = -12
(a1/a2) = 4/(3×2)= 4/6 = 2/3
(बी1/बी2) = 2/3
(c1/c2) = -8/-12 = 2/3
चूँकि (a1/a2) = (b1/b2) = (c1/c2)
ये रैखिक समीकरण संपाती रेखाएं हैं और इनके अनंत संभव समाधान हैं। इसलिए, समीकरण सुसंगत हैं।
4. रैखिक समीकरणों के निम्नलिखित में से कौन-से युग्म संगत/असंगत हैं? यदि सुसंगत है, तो रेखांकन द्वारा समाधान प्राप्त करें:
(i) x + y = 5, 2x + 2y = 10
(ii) x - y = 8, 3x - 3y = 16
(iii) 2x + y - 6 = 0, 4x - 2y - 4 = 0
(iv) 2x - 2y - 2 = 0, 4x - 4y - 5 = 0
समाधान:
(i)दिया गया है, x + y = 5 और 2x + 2y = 10
(ए1/ए2) = 1/2
(बी1/बी2) = 1/2
(सी1/सी2) = 1/2
चूँकि (a1/a2) = (b1/b2) = (c1/c2)
समीकरण संपाती होते हैं और उनके अनंत संभव हल होते हैं।
तो, समीकरण सुसंगत हैं।
के लिए, x + y = 5 या x = 5 - y

2x + 2y = 10 या x = (10-2y)/2 . के लिए

तो, समीकरणों को ग्राफ़ में निम्नानुसार दर्शाया जाता है:

आकृति से, हम देख सकते हैं कि रेखाएँ एक दूसरे को ओवरलैप कर रही हैं।
इसलिए, समीकरणों के अनंत संभव समाधान हैं।
(ii) दिया गया है, x - y = 8 और 3x - 3y = 16
(ए1/ए2) = 1/3
(बी1/बी2) = -1/-3 = 1/3
(सी1/सी2) = 8/16 = 1/2
चूँकि, (a1/a2) = (b1/b2) ≠ (c1/c2)
समीकरण एक दूसरे के समानांतर हैं और इनका कोई हल नहीं है। अतः रैखिक समीकरणों का युग्म असंगत है।
(iii) दिया गया है, 2x + y - 6 = 0 और 4x - 2y - 4 = 0
(a1/a2) = 2/4 = ½
(बी1/बी2) = 1/-2
(c1/c2) = -6/-4 = 3/2
चूँकि, (a1/a2) (b1/b2)
दिए गए रैखिक समीकरण एक दूसरे को एक बिंदु पर प्रतिच्छेद कर रहे हैं और उनका केवल एक ही हल है। अतः रैखिक समीकरणों का युग्म संगत है।
अब, 2x + y - 6 = 0 या y = 6 - 2x . के लिए

और 4x - 2y - 4 = 0 या y = (4x-4)/2 . के लिए

तो, समीकरणों को ग्राफ़ में निम्नानुसार दर्शाया जाता है:
ग्राफ से यह देखा जा सकता है कि ये रेखाएँ एक दूसरे को केवल एक बिंदु (2,2) पर प्रतिच्छेद करती हैं।
(iv) दिया गया है, 2x - 2y - 2 = 0 और 4x - 4y - 5 = 0
(a1/a2) = 2/4 = ½
(बी1/बी2) = -2/-4 = 1/2
(सी1/सी2) = 2/5
चूँकि, a1/a2 = b1/b2 c1/c2
इस प्रकार, इन रैखिक समीकरणों के समानांतर हैं और इनका कोई संभावित समाधान नहीं है। अत: रैखिक समीकरणों का युग्म असंगत है।
5. एक आयताकार बगीचे, जिसकी लंबाई उसकी चौड़ाई से 4 मीटर अधिक है, का आधा परिमाप 36 मीटर है। बगीचे के आयामों का पता लगाएं।
समाधान: आइए विचार करें।
बगीचे की चौड़ाई x और लंबाई y है।
अब, प्रश्न के अनुसार, हम दी गई शर्त को इस प्रकार व्यक्त कर सकते हैं;
वाई - एक्स = 4
तथा
वाई + एक्स = 36
अब, y - x = 4 या y = x + 4 . लेते हुए

y + x = 36 के लिए, y = 36 - x

दोनों समीकरणों का आलेखीय निरूपण इस प्रकार है;
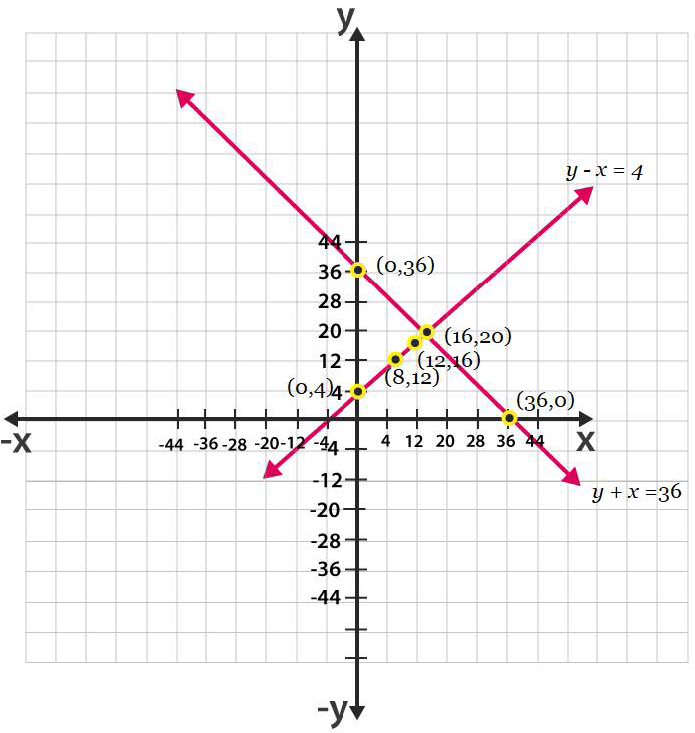
ग्राफ से आप देख सकते हैं कि रेखाएं एक दूसरे को एक बिंदु (16, 20) पर काटती हैं। अत: बगीचे की चौड़ाई 16 और लंबाई 20 है।
6. रैखिक समीकरण 2x + 3y - 8 = 0 को देखते हुए, दो चरों में एक अन्य रैखिक समीकरण इस प्रकार लिखिए कि इस प्रकार बने युग्म का ज्यामितीय निरूपण हो:
(i) प्रतिच्छेदी रेखाएं
(ii) समानांतर रेखाएं
(iii) संयोग रेखाएं
समाधान:
(i) रैखिक समीकरण 2x + 3y - 8 = 0 दिया गया है।
दो चरों में एक और रैखिक समीकरण खोजने के लिए जैसे कि गठित जोड़े का ज्यामितीय प्रतिनिधित्व प्रतिच्छेदन रेखाएं हैं, इसे नीचे की शर्त को पूरा करना चाहिए;
(a1/a2) (b1/b2)
इस प्रकार, एक अन्य समीकरण 2x - 7y + 9 = 0 हो सकता है, जैसे कि;
(a1/a2) = 2/2 = 1 और (b1/b2) = 3/-7
स्पष्ट रूप से, आप देख सकते हैं कि एक और समीकरण इस शर्त को पूरा करता है।
(ii) रैखिक समीकरण 2x + 3y - 8 = 0 दिया गया है।
दो चरों में एक और रैखिक समीकरण खोजने के लिए कि इस प्रकार बने जोड़े का ज्यामितीय प्रतिनिधित्व समानांतर रेखाएं हैं, इसे नीचे की स्थिति को पूरा करना चाहिए;
(a1/a2) = (b1/b2) ≠ (c1/c2)
इस प्रकार, एक अन्य समीकरण 6x + 9y + 9 = 0 हो सकता है, जैसे कि;
(a1/a2) = 2/6 = 1/3
(बी1/बी2) = 3/9= 1/3
(c1/c2) = -8/9
स्पष्ट रूप से, आप देख सकते हैं कि एक और समीकरण इस शर्त को पूरा करता है।
(iii) रैखिक समीकरण 2x + 3y - 8 = 0 दिया गया है।
दो चरों में एक और रैखिक समीकरण खोजने के लिए कि इस प्रकार बने जोड़े का ज्यामितीय प्रतिनिधित्व संयोग रेखाएं हैं, इसे नीचे की स्थिति को पूरा करना चाहिए;
(a1/a2) = (b1/b2) = (c1/c2)
इस प्रकार, एक अन्य समीकरण 4x + 6y - 16 = 0 हो सकता है, जैसे कि;
(a1/a2) = 2/4 = 1/2 ,(b1/b2) = 3/6 = 1/2, (c1/c2) = -8/-16 = 1/2
स्पष्ट रूप से, आप देख सकते हैं कि एक और समीकरण इस शर्त को पूरा करता है।
7. समीकरण x - y + 1 = 0 और 3x + 2y - 12 = 0 के आलेख खींचिए। इन रेखाओं और x-अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए और त्रिभुजाकार क्षेत्र को छायांकित कीजिए।
हल: दिया गया है, ग्राफ के लिए समीकरण x - y + 1 = 0 और 3x + 2y - 12 = 0 हैं।
के लिए, x - y + 1 = 0 या x = 1+y

3x + 2y - 12 = 0 या x = (12-2y)/3 . के लिए

अत: इन समीकरणों का आलेखीय निरूपण इस प्रकार है;

आकृति से, यह देखा जा सकता है कि ये रेखाएँ एक दूसरे को बिंदु (2, 3) और x-अक्ष पर (-1, 0) और (4, 0) पर प्रतिच्छेद करती हैं। अत: त्रिभुज के शीर्ष (2, 3), (-1, 0) और (4, 0) हैं।
Exercise - 3.3 पृष्ठ: 53
1. निम्नलिखित रैखिक समीकरण युग्म को प्रतिस्थापन विधि द्वारा हल कीजिए
(i) एक्स + वाई = 14
एक्स - वाई = 4
(ii) एस - टी = 3
(एस/3) + (टी/2) = 6
(iii) 3x - y = 3
9x - 3y = 9
(iv) 0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
(v) 2 x+√3 y = 0
√3 एक्स-√8 वाई = 0
(vi) (3x/2) - (5y/3) = -2
(x/3) + (y/2) = (13/6)
समाधान:
(मैंने दे दिया,
x + y = 14 और x - y = 4 दो समीकरण हैं।
पहले समीकरण से , हम प्राप्त करते हैं,
एक्स = 14 - वाई
अब, प्राप्त करने के लिए दूसरे समीकरण में x के मान को प्रतिस्थापित करें,
(14 - y) - y = 4
14 - 2y = 4
2y = 10
या वाई = 5
y के मान से, अब हम x का सटीक मान ज्ञात कर सकते हैं;
एक्स = 14 - वाई
∴ एक्स = 14 - 5
या एक्स = 9
अत: x = 9 और y = 5।
(ii) दिया गया,
s - t = 3 और (s/3) + (t/2) = 6 दो समीकरण हैं।
पहले समीकरण से , हम प्राप्त करते हैं,
एस = 3 + टी ________________(1)
अब, प्राप्त करने के लिए दूसरे समीकरण में s के मान को प्रतिस्थापित करें,
(3+टी)/3 + (टी/2) = 6
(2(3+t) + 3t )/6 = 6
(6+2t+3t)/6 = 6
(6+5t) = 36
5t = 30
t = 6
अब समीकरण (1) में t का मान प्रतिस्थापित कीजिए।
एस = 3 + 6 = 9
इसलिए, एस = 9 और टी = 6।
(iii) दिया गया,
3x - y = 3 और 9x - 3y = 9 दो समीकरण हैं।
पहले समीकरण से , हम प्राप्त करते हैं,
एक्स = (3+y)/3
अब, दिए गए दूसरे समीकरण में x के मान को प्रतिस्थापित करने के लिए,
9(3+y)/3 - 3y = 9
⇒9 +3y -3y = 9
9 = 9
इसलिए, y के अनंत मान हैं और चूंकि, x = (3+y) /3, इसलिए x के भी अनंत मान हैं।
(iv) दिया गया,
0.2x + 0.3y = 1.3 और 0.4x + 0.5y = 2.3 ये दो समीकरण हैं।
पहले समीकरण से , हम प्राप्त करते हैं,
एक्स = (1.3- 0.3y)/0.2 _________(1)
अब, दिए गए दूसरे समीकरण में x के मान को प्रतिस्थापित करने के लिए,
0.4(1.3-0.3y)/0.2 + 0.5y = 2.3
2(1.3 - 0.3y) + 0.5y = 2.3
2.6 - 0.6y + 0.5y = 2.3
2.6 - 0.1 y = 2.3
0.1 y = 0.3
वाई = 3
अब, समीकरण (1) में y के मान को प्रतिस्थापित करें, हम प्राप्त करते हैं,
x = (1.3-0.3(3))/0.2 = (1.3-0.9)/0.2 = 0.4/0.2 = 2
इसलिए, x = 2 और y = 3।
(v) दिया गया,
2 x + √3 y = 0 और √3 x - √8 y = 0
दो समीकरण हैं।
पहले समीकरण से , हम प्राप्त करते हैं,
x = - (√3/√2)y __________________(1)
दिए गए दूसरे समीकरण में x का मान रखने पर,
3(-√3/√2)y - √8y = 0 (-3/√2)y- √8 y = 0
वाई = 0
अब, समीकरण (1) में y के मान को प्रतिस्थापित करें, हम प्राप्त करते हैं,
एक्स = 0
इसलिए, x = 0 और y = 0।
(vi) दिया गया,
(3x/2)-(5y/3) = -2 और (x/3) + (y/2) = 13/6 दो समीकरण हैं।
पहले समीकरण से , हम प्राप्त करते हैं,
(3/2)x = -2 + (5y/3)
⇒ x = 2(-6+5y)/9 = (-12+10y)/9 ………………………(1)
दिए गए दूसरे समीकरण में x का मान रखने पर,
((-12+10y)/9)/3 + y/2 = 13/6
y/2 = 13/6 –((-12+10y)/27 ) + y/2 = 13/6

अब, समीकरण (1) में y के मान को प्रतिस्थापित करें, हम प्राप्त करते हैं,
(3x/2) - 5(3)/3 = -2
(3x/2) - 5 = -2
एक्स = 2
इसलिए, x = 2 और y = 3।
2. 2x + 3y = 11 और 2x - 4y = - 24 को हल कीजिए और इसलिए 'm' का वह मान ज्ञात कीजिए जिसके लिए y = mx + 3 है।
समाधान:
2x + 3y = 11………………………..(I)
2x - 4y = -24………………………… (II)
समीकरण (II) से, हम प्राप्त करते हैं
x = (11-3y)/2 ………………….(III)
समीकरण (II) में x का मान रखने पर हमें प्राप्त होता है
2(11-3y)/2 - 4y = 24
11 - 3y - 4y = -24
-7y = -35
वाई = 5 …………………………………….. (चतुर्थ)
y का मान समीकरण (III) में रखने पर, हमें प्राप्त होता है
x = (11-3×5)/2 = -4/2 = -2
अत: x = -2, y = 5
भी,
वाई = एमएक्स + 3
5 = -2 मी +3
-2 एम = 2
एम = -1
अतः m का मान -1 है।
3. निम्नलिखित समस्याओं के लिए रैखिक समीकरण युग्म बनाइए और प्रतिस्थापन विधि द्वारा उनका हल ज्ञात कीजिए।
(i) दो संख्याओं के बीच का अंतर 26 है और एक संख्या दूसरी संख्या की तीन गुनी है। उनको ढूंढो।
समाधान:
मान लीजिए कि दो संख्याएँ क्रमशः x और y हैं, जैसे कि y> x।
प्रश्न के अनुसार,
वाई = 3x ……………… (1)
वाई - एक्स = 26 ……………..(2)
(1) के मान को (2) में प्रतिस्थापित करने पर, हम प्राप्त करते हैं
3x - x = 26
एक्स = 13 ……………। (3)
(3) को (1) में रखने पर हमें y = 39 . प्राप्त होता है
अत: संख्याएँ 13 और 39 हैं।
(ii) दो संपूरक कोणों में से बड़ा कोण छोटे कोण से 18 डिग्री अधिक है। उनको ढूंढो।
समाधान:
माना x o से बड़ा कोण और छोटा कोण y o है ।
हम जानते हैं कि दो सम्पूरक कोणों का योग सदैव 180° होता है ।
प्रश्न के अनुसार,
एक्स + वाई = 180 ओ ……………। (1)
एक्स - वाई = 18 ओ ……………..(2)
(1) से, हमें x = 180 o – y …….. प्राप्त होता है। (3)
(3) को (2) में प्रतिस्थापित करने पर, हम प्राप्त करते हैं
180 o - y - y = 18 o
162 ओ = 2y
वाई = 81 ओ …………….. (4)
(3) में y के मान का प्रयोग करने पर हमें प्राप्त होता है
एक्स = 180 ओ - 81 ओ
= 99 ओ
अत: कोण 99 o और 81 o हैं ।
(iii) एक क्रिकेट टीम का कोच 7 बल्ले और 6 गेंदें 3800 रुपये में खरीदता है। बाद में, वह 1750 रुपये में 3 बल्ले और 5 गेंदें खरीदती है। प्रत्येक बल्ले और प्रत्येक गेंद का मूल्य ज्ञात कीजिए।
समाधान:
माना एक बल्ले का मूल्य x और गेंद का मूल्य y है।
प्रश्न के अनुसार,
7x + 6y = 3800 ………………। (मैं)
3x + 5y = 1750 ………………। (द्वितीय)
(I) से हमें प्राप्त होता है
वाई = (3800-7x)/6 ……………….. (III)
(II) में (II) प्रतिस्थापन (III)। हमें मिला,
3x+5(3800-7x)/6 =1750
3x+ 9500/3 - 35x/6 = 1750
3x- 35x/6 = 1750 - 9500/3
(18x-35x)/6 = (5250 - 9500)/3
-17x/6 = -4250/3
-17x = -8500
एक्स = 500 ……………………….. (चतुर्थ)
x के मान को (III) में रखने पर, हमें प्राप्त होता है
y = (3800-7 ×500)/6 = 300/6 = 50
अत: एक बल्ले की कीमत 500 रुपये और एक गेंद की कीमत 50 रुपये है।
(iv) एक शहर में टैक्सी के शुल्क में तय की गई दूरी के लिए शुल्क के साथ एक निश्चित शुल्क शामिल होता है। 10 किमी की दूरी के लिए, भुगतान किया गया शुल्क 105 रुपये है और 15 किमी की यात्रा के लिए भुगतान किया गया शुल्क 155 रुपये है। प्रति किमी निर्धारित शुल्क और शुल्क क्या हैं? 25 किमी की दूरी तय करने के लिए एक व्यक्ति को कितना भुगतान करना पड़ता है?
समाधान:
माना फिक्स चार्ज x रुपये और प्रति किमी चार्ज y रुपये है।
प्रश्न के अनुसार,
x + 10y = 105 …………….. (1)
x + 15y = 155 …………….. (2)
(1) से, हम x = 105 - 10y ……………… प्राप्त करते हैं। (3)
x के मान को (2) में रखने पर हमें प्राप्त होता है
105 - 10y + 15y = 155
5y = 50
वाई = 10 …………….. (4)
y का मान (3) में रखने पर, हमें प्राप्त होता है
एक्स = 105 - 10 × 10 = 5
अत: फिक्स चार्ज 5 रुपये है और प्रति किमी चार्ज = 10 रुपये
25 किमी के लिए शुल्क = x + 25y = 5 + 250 = रु 255
(v) एक भिन्न 9/11 हो जाती है, यदि अंश और हर दोनों में 2 जोड़ दिया जाए। यदि अंश और हर दोनों में 3 जोड़ दिया जाए तो यह 5/6 हो जाता है। अंश ज्ञात कीजिए।
समाधान:
माना भिन्न x/y है।
प्रश्न के अनुसार,
(x+2) /(y+2) = 9/11
11x + 22 = 9y + 18
11x - 9y = -4 …………….. (1)
(x+3) /(y+3) = 5/6
6x + 18 = 5y +15
6x - 5y = -3 ………………। (2)
(1) से, हमें x = (-4+9y)/11 …………….. (3) प्राप्त होता है।
x के मान को (2) में रखने पर हमें प्राप्त होता है
6(-4+9y)/11 -5y = -3
-24 + 54y - 55y = -33
-वाई = -9
वाई = 9 ………………… (4)
y के मान को (3) में रखने पर, हमें प्राप्त होता है
एक्स = (-4+9×9 )/11 = 7
अतः भिन्न 7/9 है।
(vi) पांच वर्ष बाद, जैकब की आयु उसके पुत्र की आयु की तीन गुनी होगी। पाँच वर्ष पूर्व, याकूब की आयु उसके पुत्र की आयु की सात गुनी थी। उनकी वर्तमान आयु क्या है?
समाधान:
माना याकूब और उसके पुत्र की आयु क्रमशः x और y है।
प्रश्न के अनुसार,
(एक्स + 5) = 3 (वाई + 5)
एक्स - 3y = 10 …………………………………….. (1)
(एक्स - 5) = 7 (वाई - 5)
एक्स - 7y = -30 ………………………………………। (2)
(1) से, हमें x = 3y + 10 …………….. प्राप्त होता है। (3)
x के मान को (2) में रखने पर हमें प्राप्त होता है
3y + 10 - 7y = -30
-4y = -40
वाई = 10 ………………… (4)
y के मान को (3) में रखने पर, हमें प्राप्त होता है
एक्स = 3 एक्स 10 + 10 = 40
अत: जैकब और उसके पुत्र की वर्तमान आयु क्रमशः 40 वर्ष और 10 वर्ष है।
Exercise - 3.4 पृष्ठ: 56
1. निम्न रैखिक समीकरण युग्म को विलोपन विधि और प्रतिस्थापन विधि द्वारा हल कीजिए:
(i) x + y = 5 और 2x - 3y = 4
(ii) 3x + 4y = 10 और 2x - 2y = 2
(iii) 3x - 5y - 4 = 0 और 9x = 2y + 7
(iv) x/2+ 2y/3 = -1 और xy/3 = 3
समाधान:
(i) x + y = 5 और 2x - 3y = 4
उन्मूलन की विधि द्वारा।
एक्स + वाई = 5 ………………………….. (i)
2x - 3y = 4 ………………………….. (ii)
जब समीकरण (i) को 2 से गुणा किया जाता है, तो हमें प्राप्त होता है
2x + 2y = 10 …………………………… (iii)
जब समीकरण (ii) को (iii) से घटाया जाता है, तो हमें प्राप्त होता है,
5y = 6
वाई = 6/5 ……………………………………… (iv)
y का मान eq में रखने पर। (i) हमें मिलता है,
x=5−6/5 = 19/5
x = 19/5 , y = 6/5
प्रतिस्थापन की विधि से।
समीकरण (i) से, हम प्राप्त करते हैं:
x = 5 - y………………………………….. (v)
जब मान को समीकरण (ii) में रखा जाता है, तो हमें प्राप्त होता है,
2(5 - y) - 3y = 4
-5y = -6
वाई = 6/5
जब मानों को समीकरण (v) में प्रतिस्थापित किया जाता है, तो हम प्राप्त करते हैं:
एक्स =5− 6/5 = 19/5
x = 19/5 ,y = 6/5
(ii) 3x + 4y = 10 और 2x - 2y = 2
उन्मूलन की विधि द्वारा।
3x + 4y = 10……………………….(i)
2x - 2y = 2 ………………………। (ii)
जब समीकरण (i) और (ii) को 2 से गुणा किया जाता है, तो हमें प्राप्त होता है:
4x - 4y = 4 ……………………….. (iii)
जब समीकरण (i) और (iii) को जोड़ा जाता है, तो हम प्राप्त करते हैं:
7x = 14
एक्स = 2 ……………………….(iv)
समीकरण (iv) को (i) में रखने पर हमें प्राप्त होता है,
6 + 4y = 10
4y = 4
वाई = 1
अत: x = 2 और y = 1
प्रतिस्थापन की विधि द्वारा
समीकरण (ii) से हम पाते हैं,
एक्स = 1 + वाई ………………………………… (वी)
समीकरण (v) को समीकरण (i) में रखने पर हमें प्राप्त होता है,
3(1 + y) + 4y = 10
7y = 7
वाई = 1
जब y = 1 को समीकरण (v) में प्रतिस्थापित किया जाता है, तो हमें प्राप्त होता है,
ए = 1 + 1 = 2
इसलिए, ए = 2 और बी = 1
(iii) 3x - 5y - 4 = 0 और 9x = 2y + 7
उन्मूलन की विधि द्वारा:
3x - 5y - 4 = 0 ………………………………… (i)
9x = 2y + 7
9x - 2y - 7 = 0 ………………………………… (ii)
जब समीकरण (i) और (iii) को गुणा किया जाता है, तो हमें प्राप्त होता है,
9x - 15y - 12 = 0 ……………………………… (iii)
जब समीकरण (iii) को समीकरण (ii) से घटाया जाता है, तो हमें प्राप्त होता है,
13y = -5
वाई = -5/13 ………………………………….(iv)
जब समीकरण (iv) को समीकरण (i) में प्रतिस्थापित किया जाता है, तो हमें प्राप्त होता है,
3x +25/13 −4=0
3x = 27/13
एक्स =9/13
x = 9/13 और y = -5/13
प्रतिस्थापन की विधि द्वारा:
समीकरण (i) से हम पाते हैं,
एक्स = (5y+4)/3 …………………………………………… (वी)
मान (v) को समीकरण (ii) में रखने पर हमें प्राप्त होता है,
9(5y+4)/3 −2y −7=0
13y = -5
वाई = -5/13
इस मान को समीकरण (v) में रखने पर हमें प्राप्त होता है,
एक्स = (5(-5/13)+4)/3
एक्स = 9/13
x = 9/13 , y = -5/13
(iv) x/2 + 2y/3 = -1 और xy/3 = 3
उन्मूलन की विधि द्वारा।
3x + 4y = -6 …………………………। (मैं)
xy/3 = 3
3x - y = 9 ……………………………। (ii)
जब समीकरण (ii) को समीकरण (i) से घटाया जाता है, तो हमें प्राप्त होता है,
5y = -15
वाई = -3 …………………………………। (iii)
जब समीकरण (iii) को (i) में प्रतिस्थापित किया जाता है, तो हमें प्राप्त होता है,
3x - 12 = -6
3x = 6
एक्स = 2
अत: x = 2 , y = -3
प्रतिस्थापन की विधि द्वारा:
समीकरण (ii) से हम पाते हैं,
एक्स = (वाई+9)/3…………………………………(वी)
समीकरण (v) से प्राप्त मान को समीकरण (i) में रखने पर हमें प्राप्त होता है,
3(y+9)/3 +4y =−6
5y = -15
वाई = -3
जब y = -3 को समीकरण (v) में प्रतिस्थापित किया जाता है, तो हमें प्राप्त होता है,
एक्स = (-3+9)/3 = 2
इसलिए, x = 2 और y = -3
2. निम्नलिखित समस्याओं में रैखिक समीकरणों का युग्म बनाइए और विलोपन विधि द्वारा उनके हल (यदि वे मौजूद हैं) ज्ञात कीजिए:
(i) यदि हम अंश में 1 जोड़ते हैं और हर में से 1 घटाते हैं, तो एक भिन्न घटकर 1 हो जाती है यदि हम हर में केवल 1 जोड़ते हैं। अंश क्या है?
समाधान:
माना भिन्न a/b . है
दी गई जानकारी के अनुसार,
(ए+1)/(बी-1) = 1
=> ए - बी = -2 …………………………..(i)
ए/(बी+1) = 1/2
=> 2a-b = 1…………………………………(ii)
जब समीकरण (i) को समीकरण (ii) से घटाया जाता है, तो हमें प्राप्त होता है,
ए = 3 ……………………………………………….. (iii)
जब a = 3 को समीकरण (i) में प्रतिस्थापित किया जाता है, तो हमें प्राप्त होता है,
3 - बी = -2
-बी = -5
बी = 5
अत: भिन्न 3/5 है।
(ii) पांच वर्ष पूर्व, नूरी की आयु सोनू की आयु की तीन गुनी थी। दस वर्ष बाद, नूरी की आयु सोनू से दोगुनी होगी। नूरी और सोनू कितने साल के हैं?
समाधान:
मान लीजिए, नूरी की वर्तमान आयु x . है
और सोनू की वर्तमान आयु y है।
दी गई शर्त के अनुसार, हम इस प्रकार लिख सकते हैं;
एक्स - 5 = 3 (वाई - 5)
एक्स - 3y = -10 ………………………………….. (1)
अभी,
एक्स + 10 = 2 (वाई +10)
एक्स - 2y = 10 ……………………………………। (2)
घटाना eq। 2 से 1, प्राप्त करने के लिए,
वाई = 20 ………………………………….(3)
y के मान को eq.1 में रखने पर, हम प्राप्त करते हैं,
एक्स - 3.20 = -10
एक्स - 60 = -10
एक्स = 50
इसलिए,
नूरी की उम्र 50 साल है
सोनू की उम्र 20 साल है।
(iii) दो अंकों की एक संख्या के अंकों का योग 9 है। साथ ही, इस संख्या का नौ गुना अंकों के क्रम को उलटने पर प्राप्त संख्या का दोगुना है। संख्या ज्ञात कीजिए।
समाधान:
मान लीजिए किसी संख्या का इकाई अंक और दहाई का अंक क्रमशः x और y है।
फिर, संख्या (एन) = 10 बी + ए
N अंकों के क्रम को उलटने के बाद = 10A + B
दी गई जानकारी के अनुसार, ए + बी = 9…………………….(i)
9(10बी + ए) = 2(10ए + बी)
88 बी - 11 ए = 0
-ए + 8 बी = 0 ………………………………………………………….. (ii)
समीकरण (i) और (ii) को जोड़ने पर हमें प्राप्त होता है,
9बी = 9
बी = 1……………………………………………………………………………….(3)
B के इस मान को समीकरण (i) में रखने पर हमें प्राप्त होता है A=8
अतः संख्या (N) 10B + A = 10 x 1 +8 = 18 . है
(iv) मीना 2000 रुपये निकालने के लिए एक बैंक गई। उसने कैशियर से उसे केवल 50 और 100 रुपये के नोट देने को कहा। मीना को कुल 25 नोट मिले। ज्ञात कीजिए कि उसे 50 और 100 रुपये के कितने नोट मिले।
समाधान:
मान लीजिए 50 रुपये के नोटों की संख्या A है और 100 रुपये के नोटों की संख्या B है
दी गई जानकारी के अनुसार,
ए + बी = 25 …………………………………………………………………….. (i)
50ए + 100बी = 2000 …………………………………………………………(ii)
जब समीकरण (i) को (ii) से गुणा किया जाता है, तो हमें प्राप्त होता है,
50ए + 50बी = 1250 …………………………………………………………..(iii)
समीकरण (iii) को समीकरण (ii) से घटाने पर हमें प्राप्त होता है,
50बी = 750
बी = 15
समीकरण (i) में प्रतिस्थापित करने पर हमें प्राप्त होता है,
ए = 10
अतः मीना के पास 50 रुपये के 10 नोट और 100 रुपये के 15 नोट हैं।
(v) उधार देने वाले पुस्तकालय में पहले तीन दिनों के लिए एक निश्चित शुल्क और उसके बाद प्रत्येक दिन के लिए एक अतिरिक्त शुल्क होता है। सरिता ने सात दिनों तक रखी एक किताब के लिए 27 रुपये का भुगतान किया, जबकि सूसी ने पांच दिनों तक रखी किताब के लिए 21 रुपये का भुगतान किया। प्रत्येक अतिरिक्त दिन के लिए नियत शुल्क और शुल्क ज्ञात कीजिए।
समाधान:
मान लें कि पहले तीन दिनों के लिए फिक्स चार्ज A रुपये है और प्रत्येक दिन के लिए अतिरिक्त चार्ज B रुपये है।
दी गई जानकारी के अनुसार,
ए + 4 बी = 27 ………………………………………………………………………। (मैं)
ए + 2 बी = 21 ……………………………………………………….. (ii)
जब समीकरण (ii) को समीकरण (i) से घटाया जाता है, तो हमें प्राप्त होता है,
2बी = 6
बी = 3 ……………………………………………………………………(iii)
समीकरण (i) में B = 3 रखने पर हमें प्राप्त होता है,
ए + 12 = 27
ए = 15
इसलिए, नियत शुल्क रु.15 . है
और प्रतिदिन का शुल्क 3 . रुपये है
Exercise - 3.5 पृष्ठ: 62
1. निम्न में से किस रैखिक समीकरण युग्म का अद्वितीय हल है, कोई हल नहीं है, या अपरिमित रूप से अनेक हल हैं। यदि कोई अनूठा हल है, तो उसे क्रॉस गुणन विधि का उपयोग करके खोजें।
(i) x - 3y - 3 = 0 और 3x - 9y - 2 = 0 (ii) 2x + y = 5 और 3x + 2y = 8
(iii) 3x - 5y = 20 और 6x - 10y = 40 (iv) x - 3y - 7 = 0 और 3x - 3y - 15 = 0
समाधान:
(i) दिया गया है, x - 3y - 3 =0 और 3x - 9y -2 =0
a 1 /a 2 =1/3 , b 1 /b 2 = -3/-9 =1/3, c 1 /c 2 =-3/-2 = 3/2
(ए 1 /ए 2 ) = (बी 1 /बी 2 ) (सी 1 /सी 2 )
चूँकि दी गई रेखाएँ एक-दूसरे के समानांतर हैं, वे एक-दूसरे को नहीं काटेंगी और इसलिए इन समीकरणों का कोई हल नहीं है।
(ii) दिया गया है, 2x + y = 5 और 3x +2y = 8
ए 1 /ए 2 = 2/3, बी 1 /बी 2 = 1/2, सी 1 /सी 2 = -5/-8
(ए 1 /ए 2 ) (बी 1 /बी 2 )
चूंकि वे एक अद्वितीय बिंदु पर प्रतिच्छेद करते हैं, इसलिए इन समीकरणों का क्रॉस गुणन विधि द्वारा एक अनूठा समाधान होगा:
x/(b 1 c 2 -c 1 b 2 ) = y/(c 1 a 2 – c 2 a1) = 1/(a 1 b 2 -a 2 b 1 )
x/(-8-(-10)) = y/(-15-(-16)) = 1/(4-3)
एक्स/2 = वाई/1 = 1
∴ एक्स = 2 और वाई = 1
(iii) दिया गया है, 3x - 5y = 20 और 6x - 10y = 40
(ए 1 /ए 2 ) = 3/6 = 1/2
(बी 1 /बी 2 ) = -5/-10 = 1/2
(सी 1 /सी 2 ) = 20/40 = 1/2
ए 1 /ए 2 = बी 1 /बी 2 = सी 1 /सी 2
चूँकि रेखाओं के दिए गए समुच्चय एक-दूसरे को अतिव्याप्त कर रहे हैं, इस समीकरण युग्म के लिए अनंत संख्या में हल होंगे।
(iv) दिया गया है, x - 3y - 7 = 0 और 3x - 3y - 15 = 0
(ए 1 /ए 2 ) = 1/3
(बी 1 /बी 2 ) = -3/-3 = 1
(सी 1 /सी 2 ) = -7/-15
ए 1 /ए 2 ≠ बी 1 /बी 2
चूँकि रेखाओं का यह युग्म एक दूसरे को एक अद्वितीय बिंदु पर प्रतिच्छेद कर रहा है, इसलिए एक अद्वितीय हल होगा।
क्रॉस गुणा द्वारा,
x/(45-21) = y/(-21+15) = 1/(-3+9)
x/24 = y/ -6 = 1/6
x/24 = 1/6 और y/-6 = 1/6
एक्स = 4 और वाई = 1।
2. (i) a और b के किन मानों के लिए निम्नलिखित रैखिक समीकरण युग्म के अनंत हल हैं?
2x + 3y = 7
(ए - बी) एक्स + (ए + बी) वाई = 3 ए + बी - 2
(ii) k के किस मान के लिए निम्नलिखित रैखिक समीकरण युग्म का कोई हल नहीं होगा?
3x + y = 1
(2k - 1) x + (k - 1) y = 2k + 1
समाधान:
(i) 3y + 2x -7 = 0
(ए + बी) वाई + (एबी) वाई - (3 ए + बी -2) = 0
a 1 /a 2 = 2/(ab) , b 1 /b 2 = 3/(a+b) , c 1 /c 2 = -7/-(3a + b -2)
असीम रूप से कई समाधानों के लिए,
ए 1 /ए 2 = बी 1 /बी 2 = सी 1 /सी 2
अत: 2/(ab) = 7/(3a+b-2)
6a + 2b - 4 = 7a - 7b
ए - 9बी = -4 ………………………..(i)
2/(एबी) = 3/(ए+बी)
2a + 2b = 3a - 3b
ए - 5 बी = 0 ……………………………। (ii)
(i) को (ii) से घटाने पर हमें प्राप्त होता है
4बी = 4
बी = 1
इस ईक को प्रतिस्थापित करना। (ii) में, हम प्राप्त करते हैं
ए -5 एक्स 1 = 0
ए = 5
अत: a = 5 और b = 1 पर दिए गए समीकरणों के अनंत हल होंगे।
(ii) 3x + y -1 = 0
(2k -1)x + (k-1)y - 2k -1 = 0
a 1 /a 2 = 3/(2k -1), b 1 /b 2 = 1/(k-1), c 1 /c 2 = -1/(-2k -1) = 1/( 2k +1 )
बिना किसी समाधान के
ए 1 /ए 2 = बी 1 /बी 2 ≠ सी 1 /सी 2
3/(2k-1) = 1/(k -1) ≠ 1/(2k +1)
3/(2k -1) = 1/(k -1)
3k -3 = 2k -1
कश्मीर = 2
अतः k = 2 के लिए दिए गए रैखिक समीकरण युग्म का कोई हल नहीं होगा।
3. प्रतिस्थापन और क्रॉस-गुणा विधियों द्वारा रैखिक समीकरणों के निम्नलिखित युग्म को हल करें:
8x + 5y = 9
3x + 2y = 4
समाधान:
8x + 5y = 9 …………………..(1)
3x + 2y = 4 ……………….….(2)
समीकरण (2) से हम प्राप्त करते हैं
एक्स = (4 - 2y )/3 ……………………। (3)
समीकरण 1 में इस मान का प्रयोग करते हुए, हम प्राप्त करते हैं
8(4-2y)/3 + 5y = 9
32 - 16y +15y = 27
-y = -5
वाई = 5 ………………………………….(4)
समीकरण (2) में इस मान का प्रयोग करने पर, हम प्राप्त करते हैं
3x + 10 = 4
एक्स = -2
अत: x = -2 और y = 5।
अब, क्रॉस गुणन विधि का उपयोग करना:
8x +5y - 9 = 0
3x + 2y - 4 = 0
x/(-20+18) = y/(-27 + 32 ) = 1/(16-15)
-एक्स/2 = वाई/5 =1/1
एक्स = -2 और वाई = 5।
4. निम्नलिखित समस्याओं में रैखिक समीकरण युग्म बनाइए और किसी बीजगणितीय विधि से उनके हल (यदि वे मौजूद हैं) ज्ञात कीजिए:
(i) मासिक छात्रावास शुल्क का एक हिस्सा निर्धारित किया जाता है और शेष मेस में भोजन करने के दिनों की संख्या पर निर्भर करता है। जब एक छात्र A 20 दिनों के लिए भोजन करता है, तो उसे छात्रावास शुल्क के रूप में 1000 रुपये का भुगतान करना पड़ता है, जबकि एक छात्र B, जो 26 दिनों के लिए भोजन करता है, छात्रावास शुल्क के रूप में 1180 रुपये का भुगतान करता है। निर्धारित शुल्क और प्रतिदिन भोजन की लागत ज्ञात कीजिए।
(ii) एक भिन्न 1/3 हो जाती है जब अंश में से 1 घटाया जाता है और जब उसके हर में 8 जोड़ा जाता है तो यह 1/4 हो जाता है। अंश ज्ञात कीजिए।
(iii) यश ने एक परीक्षा में 40 अंक प्राप्त किए, प्रत्येक सही उत्तर के लिए 3 अंक प्राप्त किए और प्रत्येक गलत उत्तर के लिए 1 अंक खो दिया। यदि प्रत्येक सही उत्तर के लिए 4 अंक दिए जाते और प्रत्येक गलत उत्तर के लिए 2 अंक काटे जाते, तो यश को 50 अंक प्राप्त होते। टेस्ट में कितने प्रश्न थे?
(iv) स्थान A और B एक राजमार्ग पर 100 किमी की दूरी पर हैं। एक कार A से और दूसरी B से एक ही समय पर चलना शुरू करती है। यदि कारें एक ही दिशा में अलग-अलग गति से यात्रा करती हैं, तो वे 5 घंटे में मिलती हैं। यदि वे एक दूसरे की ओर यात्रा करते हैं, तो वे 1 घंटे में मिलते हैं। दोनों कारों की गति क्या है?
(v) एक आयत का क्षेत्रफल 9 वर्ग इकाई कम हो जाता है, यदि इसकी लंबाई 5 इकाई कम कर दी जाती है और चौड़ाई 3 इकाई बढ़ा दी जाती है। यदि हम लंबाई में 3 इकाई और चौड़ाई 2 इकाई बढ़ा दें, तो क्षेत्रफल 67 वर्ग इकाई बढ़ जाता है। आयत के आयाम ज्ञात कीजिए।
समाधान:
(i) मान लीजिए कि x नियत प्रभार है और y प्रतिदिन भोजन का प्रभार है।
प्रश्न के अनुसार,
x + 20y = 1000 ……………….. (i)
x + 26y = 1180 ………………..(ii)
(i) को (ii) से घटाने पर हमें प्राप्त होता है
6y = 180
वाई = रु.30
इस मान को समीकरण (ii) में प्रयोग करने पर हमें प्राप्त होता है
एक्स = 1180 -26 x 30
एक्स = 400 रुपये।
इसलिए, निश्चित शुल्क 400 रुपये है और प्रति दिन शुल्क 30 रुपये है।
(ii) एल और भिन्न x/y हो।
तो, दिए गए प्रश्न के अनुसार,
(x -1)/y = 1/3 => 3x - y = 3 …………………(1)
x/(y + 8) = 1/4 => 4x -y =8 ………………..(2)
समीकरण (1) को (2) से घटाने पर हमें प्राप्त होता है
एक्स = 5 ………………………………….(3)
समीकरण (2) में इस मान का उपयोग करने पर, हम प्राप्त करते हैं,
(4×5)- y = 8
वाई = 12
इसलिए, भिन्न 5/12 है।
(iii) माना सही उत्तरों की संख्या x है और गलत उत्तरों की संख्या y है
दिए गए प्रश्न के अनुसार;
3x−y=40……..(1)
4x−2y=50
⇒2x−y=25…….(2)
समीकरण (2) को समीकरण (1) से घटाने पर, हम प्राप्त करते हैं;
एक्स = 15 ….….(3)
इसे समीकरण (2) में रखने पर, हम प्राप्त करते हैं;
30 - वाई = 25
या वाई = 5
अत: सही उत्तरों की संख्या = 15 और गलत उत्तरों की संख्या = 5
अत: प्रश्नों की कुल संख्या = 20
(iv) माना बिंदु A से कार की गति x किमी/घंटा है और बिंदु B से कार की गति y किमी/घंटा है।
यदि कार एक ही दिशा में चलती है,
5x - 5y = 100
एक्स - वाई = 20 ………………………………… (i)
यदि कार विपरीत दिशा में यात्रा करती है,
एक्स + वाई = 100………………………………(ii)
समीकरण (i) और (ii) को हल करने पर हमें प्राप्त होता है
एक्स = 60 किमी/घंटा ……………………………………… (iii)
इसे समीकरण (i) में प्रयोग करने पर, हम प्राप्त करते हैं,
60 - y = 20
वाई = 40 किमी/घंटा
अत: बिंदु A से कार की गति = 60 किमी/घंटा
बिंदु B से कार की गति = 40 किमी/घंटा।
(v) चलो,
आयत की लंबाई = x इकाई
तथा आयत की चौड़ाई = y इकाई
अब, दिए गए प्रश्न के अनुसार,
(x - 5) (y + 3) = xy -9
3एक्स - 5वाई - 6 = 0……………………………(1)
(x + 3) (y + 2) = xy + 67
2x + 3y - 61 = 0………………………..(2)
क्रॉस गुणन विधि का उपयोग करके, हम प्राप्त करते हैं,
x/(305 +18) = y/(-12+183) = 1/(9+10)
एक्स/323 = वाई/171 = 1/19
इसलिए, x = 17 और y = 9।
अत: आयत की लंबाई = 17 इकाई
तथा आयत की चौड़ाई = 9 इकाई
Exercise - 3.6 पृष्ठ: 67
1. समीकरणों के निम्नलिखित युग्मों को रैखिक समीकरणों के युग्म में परिवर्तित करके हल कीजिए:
(i) 1/2x + 1/3y = 2
1/3x + 1/2y = 13/6
समाधान:
मान लीजिए कि 1/x = m और 1/y = n है, तो समीकरण इस प्रकार बदल जाएगा।
एम/2 + एन/3 = 2
⇒ 3m+2n-12 = 0…………………….(1)
एम/3 + एन/2 = 13/6
⇒ 2m+3n-13 = 0……………………….(2)
अब, क्रॉस-गुणा विधि का उपयोग करके, हम प्राप्त करते हैं,
एम/(-26-(-36)) = एन/(-24-(-39)) = 1/(9-4)
एम/10 = एन/15 = 1/5
एम/10 = 1/5 और एन/15 = 1/5
तो, एम = 2 और एन = 3
1/x = 2 और 1/y = 3
एक्स = 1/2 और वाई = 1/3
(ii) 2/√x + 3/√y = 2
4/√x + 9/√y = -1
समाधान:
दिए गए समीकरणों में 1/√x = m और 1/√y = n रखने पर, हम प्राप्त करते हैं
2m + 3n = 2 ………………………..(i)
4m - 9n = -1 ……………………… (ii)
समीकरण (i) को 3 से गुणा करने पर हमें प्राप्त होता है
6 मी + 9एन = 6 …………………...(iii)
समीकरण (ii) और (iii) को जोड़ने पर, हम प्राप्त करते हैं
10मी = 5
एम = 1/2 ……………………………… (iv)
अब 'm' का मान समीकरण (i) में रखने पर, हम प्राप्त करते हैं
2×1/2 + 3n = 2
3एन = 1
एन = 1/3
एम = 1/√x
½ = 1/√x
एक्स = 4
एन = 1/√y
1/3 = 1/√y
वाई = 9
अत: x = 4 और y = 9
(iii) 4/x + 3y = 14
3/x -4y = 23
समाधान:
दिए गए समीकरण में डालने पर, हम प्राप्त करते हैं,
तो, 4m + 3y = 14 => 4m + 3y - 14 = 0 ………………..(1)
3m - 4y = 23 => 3m - 4y - 23 = 0 ……………………….(2)
क्रॉस-गुणा से, हम प्राप्त करते हैं,
मी/(-69-56) = y/(-42-(-92)) = 1/(-16-9)
-एम/125 = वाई/50 = -1/ 25
-एम/125 = -1/25 और वाई/50 = -1/25
एम = 5 और बी = -2
एम = 1/एक्स = 5
तो, एक्स = 1/5
वाई = -2
(iv) 5/(x-1) + 1/(y-2) = 2
6/(x-1) - 3/(y-2) = 1
समाधान:
दिए गए समीकरणों में 1/(x-1) = m और 1/(y-2) = n रखने पर, हम प्राप्त करते हैं,
5m + n = 2 …………………………(i)
6m - 3n = 1 ………………………। (ii)
समीकरण (i) को 3 से गुणा करने पर हमें प्राप्त होता है
15मी + 3एन = 6 ……………………….(iii)
(ii) और (iii) को जोड़ने पर हमें प्राप्त होता है
21 मी = 7
एम = 1/3
इस मान को समीकरण (i) में रखने पर, हमें प्राप्त होता है
5×1/3 + n = 2
एन = 2- 5/3 = 1/3
एम = 1/ (एक्स-1)
⇒ 1/3 = 1/(x-1)
एक्स = 4
एन = 1/(वाई-2)
⇒ 1/3 = 1/(y-2)
वाई = 5
अत: x = 4 और y = 5
(v) (7x-2y)/ xy = 5
(8x + 7y)/xy = 15
समाधान:
(7x-2y)/ xy = 5
7/y – 2/x = 5………………………..(i)
(8x + 7y)/xy = 15
8/y + 7/x = 15…………………………(ii)
दिए गए समीकरण में 1/x =m रखने पर हमें प्राप्त होता है,
- 2m + 7n = 5 => -2 + 7n - 5 = 0 …….. (iii)
7m + 8n = 15 => 7m + 8n - 15 = 0 ……(iv)
क्रॉस-गुणा विधि से, हम प्राप्त करते हैं,
मी/(-105-(-40)) = n/(-35-30) = 1/(-16-49)
एम/(-65) = एन/(-65) = 1/(-65)
मी/-65 = 1/-65
एम = 1
एन/(-65) = 1/(-65)
एन = 1
एम = 1 और एन = 1
एम = 1/एक्स = 1 एन = 1/एक्स = 1
इसलिए, x = 1 और y = 1
(vi) 6x + 3y = 6xy
2x + 4y = 5xy
समाधान:
6x + 3y = 6xy
6/y + 3/x = 6
मान लीजिए 1/x = m और 1/y = n
=> 6n +3m = 6
=>3m + 6n-6 = 0…………………….(i)
2x + 4y = 5xy
=> 2/y + 4/x = 5
=> 2n +4m = 5
=> 4m+2n-5 = 0……………………..(ii)
3m + 6n - 6 = 0
4m + 2n - 5 = 0
क्रॉस-गुणा विधि से, हम प्राप्त करते हैं
एम/(-30 -(-12)) = एन/(-24-(-15)) = 1/(6-24)
एम/-18 = एन/-9 = 1/-18
मी/-18 = 1/-18
एम = 1
एन/-9 = 1/-18
एन = 1/2
एम = 1 और एन = 1/2
एम = 1/एक्स = 1 और एन = 1/y = 1/2
एक्स = 1 और वाई = 2
अत: x = 1 और y = 2
(vii) 10/(x+y) + 2/(xy) = 4
15/(x+y) - 5/(xy) = -2
समाधान:
दिए गए समीकरणों में 1/x+y = m और 1/xy = n रखने पर, हम प्राप्त करते हैं,
10m + 2n = 4 => 10m + 2n - 4 = 0 ………………..… .. (i)
15m - 5n = -2 => 15m - 5n + 2 = 0 …………………….. (ii)
क्रॉस-गुणा विधि का उपयोग करके, हम प्राप्त करते हैं,
मी/(4-20) = एन/(-60-(20)) = 1/(-50 -30)
मी/-16 = एन/-80 = 1/-80
एम/-16 = 1/-80 और एन/-80 = 1/-80
एम = 1/5 और एन = 1
एम = 1/(एक्स+वाई) = 1/5
एक्स+वाई = 5 ……………………………………(iii)
एन = 1/(xy) = 1
xy = 1 …………………………………………… (iv)
समीकरण (iii) और (iv) को जोड़ने पर, हम प्राप्त करते हैं
2x = 6 => x = 3 …….(v)
समीकरण (3) में x = 3 का मान रखने पर, हमें प्राप्त होता है
वाई = 2
अत: x = 3 और y = 2
(viii) 1/(3x+y) + 1/(3x-y) = 3/4
1/2(3x+y) - 1/2(3x-y) = -1/8
समाधान:
दिए गए समीकरणों में 1/(3x+y) = m और 1/(3x-y) = n को प्रतिस्थापित करने पर, हम प्राप्त करते हैं,
एम + एन = 3/4 ………………………………… (1)
एम/2 - एन/2 = -1/8
एम - एन = -1/4 …………………………..…(2)
(1) और (2) को जोड़ने पर हमें प्राप्त होता है
2मी = 3/4 - 1/4
2मी = 1/2
(2) में डालने पर, हमें प्राप्त होता है
1/4 - एन = -1/4
एन = 1/4 + 1/4 = 1/2
एम = 1/(3x+y) = 1/4
3x + y = 4 …………………………………(3)
एन = 1/(3x-y) = 1/2
3x - y = 2 ………………………………(4)
समीकरण (3) और (4) को जोड़ने पर, हम प्राप्त करते हैं
6x = 6
एक्स = 1 ……………………….(5)
(3) डालने पर, हमें प्राप्त होता है
3(1) + y = 4
वाई = 1
अत: x = 1 और y = 1
2. निम्नलिखित समस्याओं को समीकरणों के युग्म के रूप में सूत्रित कीजिए और इस प्रकार उनके हल ज्ञात कीजिए:
(i) रितु धारा के अनुकूल 20 किमी 2 घंटे में और धारा के प्रतिकूल 4 किमी 2 घंटे में तैर सकती है। शांत जल में उसकी नौकायन की गति और धारा की गति ज्ञात कीजिए।
(ii) 2 महिलाएं और 5 पुरुष एक साथ कढ़ाई के काम को 4 दिनों में पूरा कर सकते हैं, जबकि 3 महिलाएं और 6 पुरुष इसे 3 दिनों में पूरा कर सकते हैं। कार्य को पूरा करने के लिए अकेले 1 महिला द्वारा लिया गया समय और अकेले 1 पुरुष द्वारा लिया गया समय ज्ञात कीजिए।
(iii) रूही अपने घर तक आंशिक रूप से ट्रेन से और आंशिक रूप से बस द्वारा 300 किमी की यात्रा करती है। यदि वह 60 किमी ट्रेन से और शेष बस द्वारा यात्रा करती है तो उसे 4 घंटे लगते हैं। यदि वह 100 किमी ट्रेन से और शेष बस द्वारा यात्रा करती है, तो उसे 10 मिनट अधिक लगते हैं। ट्रेन और बस की गति अलग-अलग ज्ञात कीजिए।
समाधान:
(i) आइए विचार करें,
शांत जल में रितु की गति = x किमी/घंटा
धारा की गति = y किमी/घंटा
अब, के दौरान रितु की गति,
डाउनस्ट्रीम = x + y किमी/घंटा
अपस्ट्रीम = x - y किमी/घंटा
दिए गए प्रश्न के अनुसार,
2(x+y) = 20
या x + y = 10……………………….(1)
और, 2(xy) = 4
या x - y = 2………………………(2)
eq.1 और 2 दोनों को जोड़ने पर, हम प्राप्त करते हैं,
2x = 12
एक्स = 6
eq.1 में x का मान रखने पर, हम प्राप्त करते हैं,
वाई = 4
इसलिए,
शांत जल में रितु नौकायन की गति = 6 किमी/घंटा
धारा की गति = 4 किमी/घंटा
(ii) आइए विचार करें,
महिलाओं द्वारा कार्य समाप्त करने में लिए गए दिनों की संख्या = x
पुरुषों द्वारा कार्य समाप्त करने में लिए गए दिनों की संख्या = y
महिलाओं द्वारा एक दिन में किया गया कार्य = 1/x
महिलाओं द्वारा एक दिन में किया गया कार्य = 1/y
दिए गए प्रश्न के अनुसार,
4(2/x + 5/y) = 1
(2/x + 5/y) = 1/4
और, 3(3/x + 6/y) = 1
(3/x + 6/y) = 1/3
अब, 1/x=m और 1/y=n रखें, हम पाते हैं,
2m + 5n = 1/4 => 8m + 20n = 1………………(1)
3मी + 6एन =1/3 => 9मी + 18एन = 1………………….(2)
अब, क्रॉस गुणन विधि से, हम यहाँ प्राप्त करते हैं,
मी/(20-18) = n/(9-8) = 1/ (180-144)
एम/2 = एन/1 = 1/36
एम/2 = 1/36
एम = 1/18
एम = 1/एक्स = 1/18
या एक्स = 18
एन = 1/y = 1/36
वाई = 36
इसलिए,
महिलाओं द्वारा कार्य समाप्त करने में लिए गए दिनों की संख्या = 18
पुरुषों द्वारा कार्य समाप्त करने में लिए गए दिनों की संख्या = 36.
(iii) आइए विचार करें,
ट्रेन की गति = x किमी/घंटा
बस की गति = y किमी/घंटा
दिए गए प्रश्न के अनुसार,
60/x + 240/y = 4 …………………(1)
100/x + 200/y = 25/6 …………….(2)
उपरोक्त दो समीकरणों में 1/x=m और 1/y=n रखें;
60मी + 240एन = 4……………………..(3)
100मी + 200एन = 25/6
600 मीटर + 1200एन = 25 ………………….(4)
प्राप्त करने के लिए eq.3 को 10 से गुणा करें,
600 मीटर + 2400एन = 40 ……………………(5)
अब, प्राप्त करने के लिए, 5 से eq.4 घटाएं,
1200एन = 15
एन = 15/1200 = 1/80
n के मान को eq में रखिए। 3, पाने के लिए,
60 मी + 3 = 4
एम = 1/60
एम = 1/एक्स = 1/60
एक्स = 60
और वाई = 1/एन
वाई = 80
इसलिए,
ट्रेन की गति = 60 किमी/घंटा
बस की गति = 80 किमी/घंटा
Exercise - 3.7 पृष्ठ: 68
1. दो मित्रों अनी और बीजू की आयु में 3 वर्ष का अंतर है। अनी के पिता धरम की आयु अनी से दोगुनी है और बीजू की आयु अपनी बहन कैथी से दोगुनी है। कैथी और धरम की आयु में 30 वर्ष का अंतर है। अनी और बीजू की आयु ज्ञात कीजिए।
समाधान:
अनी और बीजू की आयु का अंतर 3 वर्ष है।
या तो बीजू, अनी से 3 साल बड़ा है या अनी बीजू से 3 साल बड़ा है। दोनों ही स्थितियों से हमें पता चलता है कि अनी के पिता की आयु कैथी की आयु से 30 वर्ष अधिक है।
माना अनी और बीजू की आयु क्रमशः A और B है।
अत: धरम की आयु = 2 x A = 2A वर्ष।
और बीजू बहन ऐन की उम्र बी/2 साल
दी गई जानकारी का उपयोग करके,
केस (i)
जब अनी बीजू से 3 वर्ष बड़ा होता है तो A - B = 3 - - - - - - - - (1)
2A−B/2 = 30
4ए - बी = 60 - - - - - - - - - - - (2)
समीकरणों (1) और (2) को घटाकर, हम प्राप्त करते हैं,
3ए = 60 - 3 = 57
ए = 57/3 = 19
अत: अनी की आयु = 19 वर्ष
और बीजू की आयु 19 - 3 = 16 वर्ष है।
मामला (ii)
जब बीजू अनी से बड़ा है,
बी - ए = 3 - - - - - - - - (1)
2ए - बी/2 = 30
4ए - बी = 60 - - - - - - - - (2)
समीकरण (1) और (2) को जोड़ने पर हमें प्राप्त होता है,
3ए = 63
ए = 21
अत: अनी की आयु 21 वर्ष है
और बीजू की आयु 21 + 3 = 24 वर्ष है।
2. एक कहता है, "मुझे सौ दो, मित्र! तब मैं तुमसे दुगना धनवान बन जाऊँगा।" दूसरा जवाब देता है, "यदि आप मुझे दस देते हैं, तो मैं आपके जितना अमीर छह गुना हो जाऊंगा"। मुझे बताओ कि उनकी (संबंधित) पूंजी की राशि क्या है? [भास्कर II के बीजगणित से] [संकेत : x + 100 = 2 (y – 100), y + 10 = 6 (x – 10)]।
समाधान:
माना संगम के पास A रुपये हैं और रूबेन के पास B रुपये हैं।
दी गई जानकारी का उपयोग करके हम प्राप्त करते हैं,
ए + 100 = 2 (बी - 100) ⇒ ए + 100 = 2 बी - 200
या ए - 2 बी = -300 - - - - - - - (1)
और
6(ए - 10) = (बी + 10)
या 6ए - 60 = बी + 10
या 6ए - बी = 70 - - - - - - (2)
जब समीकरण (2) को 2 से गुणा किया जाता है, तो हमें प्राप्त होता है,
12ए - 2बी = 140 - - - - - - - (3)
जब समीकरण (1) को समीकरण (3) से घटाया जाता है, तो हमें प्राप्त होता है,
11ए = 140 + 300
11ए = 440
ए = 440/11 = 40
समीकरण (1) में A = 40 का प्रयोग करने पर हमें प्राप्त होता है,
40 - 2बी = -300
40 + 300 = 2बी
2बी = 340
बी = 170
अत: संगम के पास 40 रुपये और रूबेन के पास 170 रुपये थे।
3. एक ट्रेन एक समान गति से एक निश्चित दूरी तय करती है। यदि ट्रेन 10 किमी/घंटा तेज होती, तो उसे निर्धारित समय से 2 घंटे कम समय लगता। और, यदि ट्रेन 10 किमी/घंटा धीमी थी; यह निर्धारित समय से 3 घंटे अधिक लेता। ट्रेन द्वारा तय की गई दूरी ज्ञात कीजिए।
समाधान:
माना ट्रेन की गति A किमी/घंटा है और ट्रेन द्वारा दूरी तय करने में लिया गया समय N घंटे है और यात्रा करने के लिए दूरी X घंटे है।
ट्रेन की गति = ट्रेन द्वारा तय की गई दूरी / उस दूरी को तय करने में लगा समय
ए = एन (दूरी) / एक्स (समय)
या, एन = कुल्हाड़ी - - - - - - - - - - (1)
दी गई जानकारी का उपयोग करते हुए, हम प्राप्त करते हैं:
(ए+10) = एक्स/(एन-2)
(ए + 10) (एन - 2) = एक्स
एएन + 10N - 2A - 20 = X
समीकरण (1) का उपयोग करके हम प्राप्त करते हैं,
- 2ए + 10एन = 20 - - - - - - - - - - (2)
(ए-10) = एक्स/(एन+3)
(ए - 10) (एन + 3) = एक्स
एएन - 10एन + 3ए - 30 = एक्स
समीकरण (1) का उपयोग करके हम प्राप्त करते हैं,
3ए - 10एन = 30 - - - - - - - - - (3)
समीकरण (2) और समीकरण (3) को जोड़ने पर हमें प्राप्त होता है,
ए = 50
समीकरण (2) का उपयोग करके हम प्राप्त करते हैं,
(-2) एक्स (50) + 10एन = 20
-100 +10N = 20
=> 10एन = 120
एन = 12 घंटे
समीकरण (1) से हम पाते हैं,
ट्रेन द्वारा तय की गई दूरी, X = AN
= 50 x 12
= 600 किमी
अत: ट्रेन द्वारा तय की गई दूरी 600km है।
4. एक कक्षा के विद्यार्थियों को पंक्तियों में खड़ा किया जाता है। यदि एक पंक्ति में 3 विद्यार्थी अतिरिक्त हों, तो 1 पंक्ति कम होगी। यदि एक पंक्ति में 3 विद्यार्थी कम हों, तो 2 पंक्तियाँ अधिक होंगी। कक्षा में छात्रों की संख्या ज्ञात कीजिए।
समाधान:
मान लीजिए पंक्तियों की संख्या A है और एक पंक्ति में विद्यार्थियों की संख्या B है।
विद्यार्थियों की कुल संख्या = पंक्तियों की संख्या x एक पंक्ति में विद्यार्थियों की संख्या
=एबी
दी गई जानकारी का उपयोग करते हुए,
पहली शर्त:
छात्रों की कुल संख्या = (ए -1) (बी + 3)
या एबी = (ए -1) (बी + 3) = एबी - बी + 3 ए - 3
या 3ए - बी - 3 = 0
या 3ए - वाई = 3 - - - - - - - - - - - - (1)
दूसरी शर्त:
छात्रों की कुल संख्या = (ए + 2) (बी - 3)
या AB = AB + 2B - 3A - 6
या 3ए - 2 बी = -6 - - - - - - - - - (2)
जब समीकरण (2) को (1) से घटाया जाता है
(3ए - बी) - (3 ए - 2 बी) = 3 - (-6)
-बी + 2 बी = 3 + 6 बी = 9
समीकरण (1) का उपयोग करके हम प्राप्त करते हैं,
3ए - 9 =3
3ए = 9+3 = 12
ए = 4
पंक्तियों की संख्या, ए = 4
एक पंक्ति में विद्यार्थियों की संख्या, B = 9
एक कक्षा में कुल विद्यार्थियों की संख्या = AB = 4 x 9 = 36
5. एक ABC में, C = 3 ∠ B = 2 (∠A + B) है। तीन कोण खोजें।
समाधान:
दिया गया,
C = 3 B = 2(∠B + A)
3∠B = 2 A+2 B
बी=2 ए
2∠A - ∠B = 0- - - - - - - - - - - (i)
हम जानते हैं कि त्रिभुज के सभी अंतः कोणों का योग 180 O होता है ।
अत: A +∠B+ C = 180 O
A + B +3 B = 180 O
A + 4 ∠B = 180 O - - - - - - - - - - - - - - (ii)
4 को समीकरण (i) से गुणा करने पर, हमें प्राप्त होता है
8 A - 4 B = 0- - - - - - - - - - - (iii)
समीकरण (iii) और (ii) को जोड़ने पर हमें प्राप्त होता है
9 A = 180 O
ए = 20 ओ
इसे समीकरण (ii) में प्रयोग करने पर, हम प्राप्त करते हैं
20 ओ + 4∠बी = 180 ओ
बी = 40 ओ
3∠बी =∠सी
सी = 3 x 40 = 120 ओ
इसलिए, A = 20 O
बी=40 ओ
सी = 120 ओ
6. समीकरण 5x - y = 5 और 3x - y = 3 के आलेख खींचिए। इन रेखाओं और y अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए।
समाधान:
दिया गया,
5x - y = 5
=> y = 5x - 5
इसकी समाधान तालिका होगी।

3x - y = 3 . भी दिया गया है
वाई = 3x - 3

इन पंक्तियों का चित्रमय निरूपण इस प्रकार होगा:

उपरोक्त ग्राफ से हम देख सकते हैं कि बनने वाला त्रिभुज रेखाओं और y अक्ष से ABC है। साथ ही शीर्षों के निर्देशांक A(1,0) , C(0,-5) और B(0,-3) हैं।
7. रैखिक समीकरणों के निम्नलिखित युग्म को हल कीजिए:
(i) px + qy = p – q
qx - py = p + q
(ii) कुल्हाड़ी + बाय = सी
बीएक्स + एई = 1 + सी
(iii) x/a – y/b = 0
कुल्हाड़ी + बाय = ए 2 + बी 2
(iv) (a - b)x + (a + b) y = a 2 - 2ab - b 2
(ए + बी) (एक्स + वाई) = ए 2 + बी 2
(v) 152x - 378y = - 74
-378x + 152y = - 604
समाधान:
(i) px + qy = p – q……………(i)
qx - py = p + q……………………..(ii)
p को समीकरण (1) और q को समीकरण (2) में गुणा करने पर, हम प्राप्त करते हैं
पी 2 एक्स + पीक्यूई = पी 2 - पीक्यू …………… (iii)
क्यू 2 एक्स - पीक्यूवाई = पीक्यू + क्यू 2 …………… (iv)
समीकरण (iii) और समीकरण (iv) को जोड़ने पर, हम प्राप्त करते हैं
पी 2 एक्स + क्यू 2 एक्स = पी 2 + क्यू 2
(पी 2 + क्यू 2 ) एक्स = पी 2 + क्यू 2
एक्स = (पी 2 + क्यू 2 )/ पी 2 + क्यू 2 = 1
समीकरण (i) से, हम प्राप्त करते हैं
p(1) + qy = p – q
क्यूई = पीक्यूपी
क्यू = -क्यू
वाई = -1
(ii) ax + by= c………………………(i)
बीएक्स + एई = 1+ सी …………… ..(ii)
समीकरण (i) और b को समीकरण (ii) से गुणा करने पर, हम प्राप्त करते हैं
a 2 x + aby = ac ………………… (iii)
बी 2 एक्स + एबी = बी + बीसी …………… (iv)
समीकरण (iv) को समीकरण (iii) से घटाना,
(ए 2 - बी 2 ) एक्स = एसी - बीसी- बी
एक्स = (एसी - बीसी- बी)/ (ए 2 - बी 2 )
x = c(ab) –b / (a 2 +b 2 )
समीकरण (i) से, हम प्राप्त करते हैं
कुल्हाड़ी +द्वारा = सी
a{c(a−b)−b)/ (a 2 – b 2 )} +by=c
ac(a−b)−ab/ (a 2 - b 2 )+by=c
by=c–ac(a−b)−ab/(a 2 – b 2 )
by=abc - b 2 c+ab/a 2 -b 2
वाई = सी(एबी)+ए / ए 2 -बी 2
(iii) x/a – y/b = 0
कुल्हाड़ी + बाय = ए 2 + बी 2
एक्स/ए - वाई/बी = 0
=> बीएक्स - एई = 0 ……। (मैं)
ax + by = a 2 + b 2 …….. (ii)
समीकरण (i) और (ii) में क्रमशः a और b को गुणा करने पर, हम प्राप्त करते हैं
बी 2 एक्स - अबी = 0 …………… (iii)
a 2 x + aby = a 3 + ab 3 …… (iv)
समीकरण (iii) और (iv) को जोड़ने पर, हम प्राप्त करते हैं
बी 2 एक्स + ए 2 एक्स = ए 3 + एबी 2
एक्स (बी 2 + ए 2 ) = ए (ए 2 + बी 2 ) एक्स = ए
समीकरण (i) का प्रयोग करते हुए, हम प्राप्त करते हैं
बी (ए) - एई = 0
एबी - एई = 0
अय = अब,
वाई = बी
(iv) (a - b)x + (a + b) y = a 2 - 2ab - b 2
(ए + बी) (एक्स + वाई) = ए 2 + बी 2
(ए + बी) वाई + (ए - बी) एक्स = ए 2 - 2ab - बी 2 …………… (i)
(एक्स + वाई) (ए + बी) = ए 2 + बी 2
(ए + बी) वाई + (ए + बी) एक्स = ए 2 + बी 2 ………………… (ii)
समीकरण (ii) को समीकरण (i) से घटाने पर हमें प्राप्त होता है
(ए - बी) एक्स - (ए + बी) एक्स = (ए 2 - 2ab - बी 2 ) - (ए 2 + बी 2 )
x(a - b - a - b) = - 2ab - 2b 2
− 2bx = - 2b (b + a)
एक्स = बी + ए
इस मान को समीकरण (i) में रखने पर हमें प्राप्त होता है
(a + b)(a - b) +y (a + b) = a 2 - 2ab - b 2
a 2 - b 2 + y(a + b) = a 2 - 2ab - b 2
(ए + बी) वाई = -2ab
वाई = -2ab/(ए+बी)
(v) 152x - 378y = - 74
76x - 189y = - 37
x =(189y-37)/76……………..…(i)
− 378x + 152y = -604
− 189x + 76y = -302 …………….. (ii)
समीकरण (ii) में x के मान का प्रयोग करने पर हमें प्राप्त होता है
−189(189y−37)/76+76y=−302
- (189) 2 y + 189 × 37 + (76) 2 y = - 302 × 76
189 × 37 + 302 × 76 = (189) 2 y - (76) 2 y
6993 + 22952 = (189 - 76) (189 + 76) y
29945 = (113) (265) वाई
वाई = 1
समीकरण (i) का प्रयोग करते हुए, हम प्राप्त करते हैं
एक्स = (189-37)/76
एक्स = 152/76 = 2
8. ABCD एक चक्रीय चतुर्भुज है (देखिए आकृति 3.7)। चक्रीय चतुर्भुज के कोण ज्ञात कीजिए।

समाधान:
यह ज्ञात है कि एक चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है
इस प्रकार, हमारे पास है
सी +∠ए = 180
4y + 20− 4x = 180
− 4x + 4y = 160
x - y = - 40 ……………(1)
और, B + ∠D = 180
3y - 5 - 7x + 5 = 180
− 7x + 3y = 180 ………..(2)
3 को समीकरण (1) से गुणा करने पर, हम प्राप्त करते हैं
3x - 3y = - 120 ………(3)
समीकरण (2) को समीकरण (3) में जोड़ने पर, हम प्राप्त करते हैं
- 7x + 3x = 180 - 120
− 4x = 60
एक्स = -15
इस मान को समीकरण (i) में रखने पर हमें प्राप्त होता है
एक्स - वाई = - 40
-y−15 = − 40
वाई = 40-15
= 25
A = 4y + 20 = 20+4(25) = 120°
∠B = 3y - 5 = - 5+3(25) = 70°
C = -4x = -4(− 15) = 60°
डी = 5-7x
D= 5− 7(−15) = 110°
इसलिए, सभी कोणों को मापा जाता है।












